• Naturaleza: El crecimiento en la naturaleza obedece en multitud de casos a un orden muy especial determinado por la famosa sucesión de números: 1, 1, 3, 5, 8, 13, 21, 24, ... llamada sucesión de Fibonacci.

  • Disposición de Fibonacci en las semillas de girasol

  

  • Esta sucesión aparece en botánica en el estudio de la disposición de las hojas (filotaxia). Los brotes y hojas de los árboles surgen a diferentes ángulos. Se ha verificado que en el manzano y el roble, por ejemplo, una espiral trazada en torno a la rama pasa por 5 brotes cada 2 vueltas completas, en el álamo y el peral, una espiral de 3 vueltas pasa por 8 brotes. Las escamas de una piña de pino están dispuestas en 5 hileras que corren hacia arriba y a la derecha y 8 que lo hacen a la izquierda. Las cabezas de las margaritas y los girasoles suelen tener 21 espirales creciendo en una dirección y 34 en la otra. Más información en http://www.mcs.surrey.ac.uk/Personal/R.Knott/Fibonacci/fibnat.html#petals

  • Las abejas también tienen relación con las series de Fibonacci: si se observan las celdas hexagonales de una colmena y se coloca a una abeja en una cualquiera de ellas, y se le permite alimentar a la larva, suponiendo que continuará siempre por la celda contigua de la derecha, veremos que hay sólo una ruta posible para la siguiente celdilla; dos hacia la segunda, tres hasta la tercera, cinco hasta la cuarta, ocho rutas posibles hacia la quinta, etcétera.

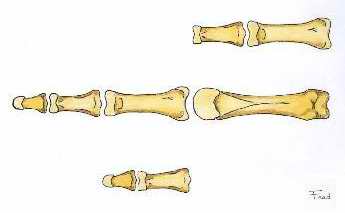
  • En la mano humana: la longitud del metacarpo es la suma de las dos falanges proximales. La longitud de la primera falange es la suma de las dos falanges distales.

• Si se toma un grupo de fichas de dominó, de tamaño 2 x 1, la cantidad de maneras de construir rectángulos de tamaño 2 x n será, por supuesto, una serie de Fibonacci. Hay una sola forma de armar un rectángulo de 2 x 1; dos de construir el de 2 x 2; tres de hacer el de 2 x 3, cinco para el de 2 x 4; ocho para el de 2 x 5, etc.

• Literatura. En el siguiente fragmento de El código Da Vinci aparece la sucesión de Fibonacci como sucesión misteriosa en la resolución de un enigma.

• Física: También la física parece adorar las sucesiones de Fibonacci. Si se colocan dos láminas planas de vidrio en contacto y se hace que unos rayos luminosos las atraviesen, algunos (dependiendo del ángulo de incidencia) las atravesarán sin reflejarse, pero otros sufrirán una reflexión. El rayo que no sufre reflexión tiene sólo una trayectoria posible de salida; el que sufre una reflexión tiene dos rutas posibles; el que sufre dos reflexiones, tres trayectorias, el que experimenta tres reflexiones, cinco, y así sucesivamente. Tenemos aquí nuevamente una serie de Fibonacci: 1, 1, 2, 3, 5, 8...

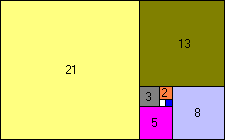
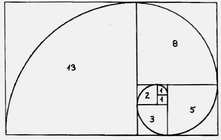
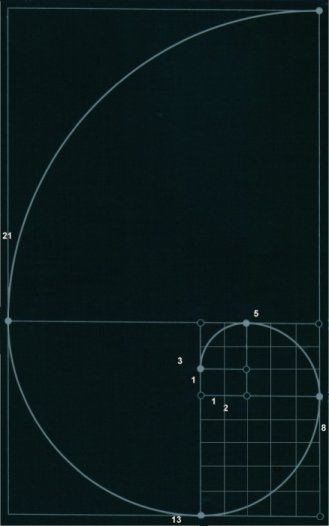
• Rectángulos de Fibonacci: Comenzamos dibujando dos pequeños cuadrados de lado una unidad, que estén juntos, a partir de ahí se forma un rectángulo, cuyo lado mayor  que es 2 sirve como lado de un nuevo cuadrado , el cual pegamos a los anteriores, nuevamente obtenemos un rectángulo de dimensiones 3 x 2; a partir de aquí, el proceso se reitera, sucesivamente, añadiendo cuadrados cuyos lados son los números de la sucesión de Fibonacci...
  Lógicamente, cada cuadrado tiene como lado, la suma de los lados de los dos cuadrados construidos anteriormente....Los sucesivos rectángulos que van apareciendo son los rectángulos de Fibonacci. De un rectángulo se deriva la espiral de Fibonacci. Esta curva ha cautivado, por su belleza y propiedades, la atención de matemáticos, artistas y naturalistas. Puedes pulsar aquí para ver algunos ejemplos.