De las definiciones de razones trigonométricas de un ángulo cualquiera, se deduce:

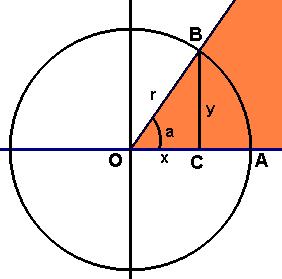
sen α = y r  ⇒  sen 2  α = y 2 r 2 cos α = x r  ⇒  cos 2  α = x 2 r 2 Sumando ordenadamente y considerando el teorema de Pitágoras en el triángulo OCB , obtenemos la fórmula del Teorema Fundamental de la Trigonometría: sen 2  α  +cos 2  α =  y 2 r 2 +  x 2 r 2 = y 2 +x 2 r 2 = r 2 r 2 =1

Reuniendo esta fórmula con las que se obtienen de las definiciones anteriores, se deduce el siguiente grupo de relaciones llamadas fundamentales:

[ 1 ]  sen 2  α  +cos 2  α = 1   [ 2 ] tg α = sen α  cos α     [ 3 ] cosec α =  1 sen α    ​   [ 4 ] sec α =  1 cos α    ​   [ 5 ] ctg α =  cos α sen α

Del Teorema Fundamental de la Trigonometría se deducen las siguientes fórmulas:

[ 1a ] 1+ ctg 2  α =  1 sen 2  α    o   1+ ctg 2  α  = cosec 2  α  [ 1b ] 1+ tg 2  α =  1 cos 2  α    o   1+ tg 2  α  = sec 2  α