Todo ángulo AÔB= a puede referirse a un sistema de coordenadas cartesianas rectangulares,
de modo que su vértice coincida con el origen de coordenadas y el lado origen con el semieje
positivo OX.
El lado extremo ocupará una posición cualquiera, y el cuadrante en que esté situado se dirá que
es el cuadrante al cual pertenece el ángulo.
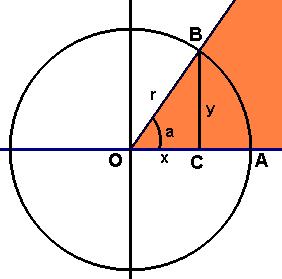
Consideremos una circunferencia de radio r y centro O. Esta circunferencia corta
al lado extremo del ángulo en un punto B, que tiene de abscisa OC= x y de ordenada BC = y
|
|