La medición "directa" de alturas y distancias es una operación que resulta a menudo difícil y, a veces, imposible. No sucede lo mismo cuando se trata de ángulos, ya que su medida se logra con facilidad y exactitud, merced a aparatos especiales como el TEODOLITO (mide ángulos horizontales y verticales).
Sin embargo, es posible la medición "indirecta" de distancias basándonos en la resolución de triángulos.

1.- Determinación de la altura de un punto de pie accesible.

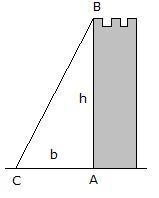
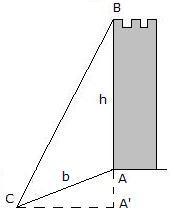
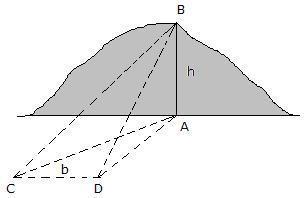
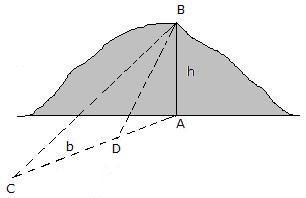
Si se trata, por ejemplo, de medir la altura de una torre vertical cuya base A es accesible, se elige sobre el terreno una base AC=b que sea horizontal. Del triángulo rectángulo formado se deduce h = b tg C

Si la base AC no es horizontal, se puede medir, además de la base AC y el ángulo BCA, el ángulo BCA’, porque los teodolitos van provistos de niveles. ABC=90º-BCA' ⇒  h sen BCA = b sen ABC ⇒h =  b sen BCA cos BCA'

   

2.- Cálculo de la altura de un punto de pie inaccesible. (Método de doble observación)

Para determinar la altura h de una montaña respecto del plano horizontal que pasa por un punto C de la superficie, se toma una base auxiliar CD que sea horizontal: Colocando el teodolito en C y D se miden los ángulos horizontales ACD y ADC, lo que permite calcular AC b sen CAD  = AC sen ADC   donde    sen CAD = sen ( 180º-(ADC+ACD) )=sen (ADC+ACD) AC =  b sen ADC sen(ADC+ACD) ⇒ h = AC tg BCA =  b sen ADC · tg BCA  sen(ADC+ACD)

Si la base CD estuviera sobre CA, el cálculo sería más sencillo. Colocando el teodolito en C y D se miden los ángulos verticales ACB y ADB. tg ACB = h CD+DA    tg ADB =  h DA ⇒ DA = h tg ADB tg ACB = h CD+ h tg ADB   ⇒h =  tg ACB · CD 1 -  tg ACB tg ADB

---