A las expresiones que ya conocemos del área de un triángulo, la Trigonometría añade algunas otras.

a) Anotamos en primer lugar la conocida:
S =  1 2 a h 1   S =  1 2 b h 2   S =  1 2 c h 3  (*)

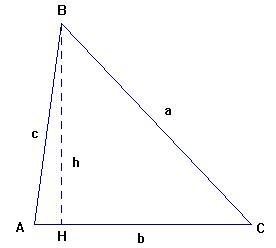
"El área de un triángulo es igual al semiproducto de la base y la altura".

b) Sea el triángulo ABC, siendo h la altura correspondiente al lado b.

En el triángulo CHB se verifica que: h= a sen C. Luego sustituyendo en (*) se obtiene:

S =  1 2  a b sen C

Si en lugar de haber considerado la altura correspondiente al lado b, hubiéramos considerado las otras dos alturas, obtendríamos:

S =  1 2 a c sen B  ;  S =  1 2  b c sen A

"El área de un triángulo es igual al semiproducto de dos de sus lados por el seno del ángulo que forman"

c) Según el teorema del seno: c sen C    =   2 R      De ahí se deduce que sen C =  c 2 R      

Si lo sustituimos en S= 1 2 a b sen C = 1 2 a b  c 2R      Luego S =  a b c 4 R

"El área de un triángulo es igual al producto de sus tres lados dividido por 4 veces el radio de su circunferencia circunscrita"

d) FÓRMULA DE HERÓN. Desde el siglo I de nuestra era es conocida una fórmula para el cálculo del área del triángulo en la que aparecen sólo la medida de los lados.

Esta expresión fue encontrada por Herón de Alejandría y recibe el nombre de fórmula de Herón.

S =   p (p-a) (p-b) (p-c) donde  p= a+b+c 2   (semiperímetro)