1. Decir cuáles de las siguientes sucesiones son monótonas y
cuáles no cumplen esta propiedad, sabiendo que sus términos generales son:
an = (-
2)n ; bn = -
2n ; cn = 2-n
Las sucesiones (an) y (bn)
son monótonas estrictamente crecientes y (cn) es monótona
estrictamente decreciente
La sucesión (an) es monótona
estrictamente creciente, (bn) y (cn) son monótonas
estrictamente decrecientes
La
sucesión (an) no es monótona, (bn) y (cn) son
monótonas estrictamente decrecientes
La sucesión (an) no es
monótona, (bn) es monótona estrictamente creciente y (cn)
es monótona estrictamente decreciente
|
2. Se considera (an) la sucesión de las áreas de los
círculos inscritos en los hexágonos regulares cuyo lado mide n cm. Sea (bn)
la sucesión de las áreas de los círculos inscritos en los triángulos
equiláteros cuyo lado mide 3n cm. Demostrar que la sucesión diferencia de
las dos anteriores (an - bn), verifica alguna de las
siguientes propiedades:
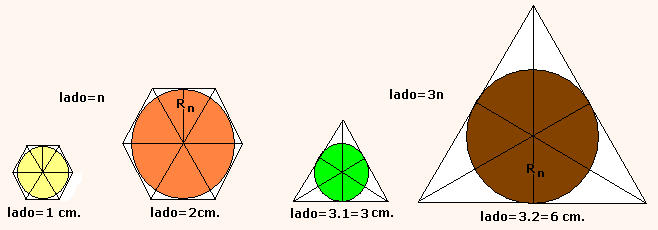
La sucesión (an-
bn) es monótona estrictamente decreciente
La sucesión (an-
bn) es monótona estrictamente creciente
La sucesión (an-
bn) no es monótona
La sucesión (an-
bn) es una sucesión constante
|
3. Dadas las siguientes sucesiones monótonas, estudiar si son
crecientes o decrecientes:
a
n
=
n
2n+5
;
b
n
=
n+4
n
;
c
n
=
5n+4
3n−1
(an)
y (cn) son monótonas estrictamente decrecientes y (bn) es
estrictamente creciente
(an)
es monótona estrictamente creciente, (bn) y (cn)
son estrictamente decrecientes
(an)
y (bn) son monótonas estrictamente crecientes y (cn) es estrictamente decreciente
(an)
es monótona estrictamente decreciente, (bn) y (cn)
son estrictamente crecientes
|
4. Dados los términos generales de las siguientes sucesiones, demostrar si
son monótonas o no lo son:
a
n
=cos (
n π
2
)
;
b
n
=
n+1
5n+3
La sucesión (an) no es monótona y la sucesión (bn) es estrictamente creciente
La sucesión (an) es
monótona estrictamente creciente y la sucesión (bn) no es
monótona
Las sucesiones (an) y (bn)
son monótonas estrictamente decrecientes
La sucesión (an) no es monótona y la sucesión (bn) es estrictamente decreciente
|
5. Estudiar si la sucesión que tiene el término general siguiente
es una sucesión monótona y, en el caso de que sea así, demostrar si es
creciente o decreciente
a
n
=
1.3.5...(2n−1)
2.4.6...(2n)
La sucesión (an) es monótona estrictamente decreciente
La sucesión (an) no es
monótona
La sucesión (an) es
monótona estrictamente creciente
La sucesión (an) es monótona decreciente
|
6. Estudiar si 2 es cota inferior de la sucesión cuyo término
general es
a
n
=
1−6n
−2n
la sucesión (an) no está
acotada inferiormente
2 no es cota de la sucesión (an),
aunque ésta es acotada
2 es cota superior de la sucesión (an)
2 es cota inferior de la sucesión (an)
|
7. Dada la sucesión cuyo término general es
a
n
=
1+4n
3+n
. Demostrar si
las siguientes propiedades son verdaderas o falsas
a) 4 es cota superior de (an)
b) 3'999999 es cota superior de (an)
a) falsa ;
b) verdadera
a) verdadera ; b) falsa
a) verdadera ; b) verdadera
a) falsa ; b) falsa
|
8. Estudiar si las sucesiones cuyo término general definimos
seguidamente son sucesiones acotadas o no:
a
n
=
4
n
;
b
n
=−2n+1 ;
c
n
=
n
;
d
n
=
n−6
2
(an) y (bn)
no están acotadas inferiormente, (cn) y (dn) no están
acotadas superiormente
(an) está acotada, (bn)
y (dn) no están acotadas inferiormente y (cn) no
está acotada superiormente
(an)
está acotada, (bn) no está acotada inferiormente, (cn) y
(dn) no están acotadas superiormente
(an) y (bn)
están acotadas, (cn) no está acotada inferiormente y (dn)
no está acotada superiormente
|
9. Estudiar si 2 es cota superior de la sucesión cuyos cuatro
primeros términos son
{
6
5
,
12
11
,
24
23
,
48
47
, ...
}
la sucesión no está acotada superiormente
2 es cota superior de la sucesión
2 no es cota superior de la sucesión, aunque está acotada
superiormente
la sucesión no está acotada ni superior ni inferiormente
|
10. Estudiar si la sucesión, de la cual definimos seguidamente los
cuatro primeros términos, es acotada o no
{
−
1
5
,
1
9
,
3
13
,
5
17
, ...
}
La sucesión está acotada
La sucesión está acotada únicamente superiormente
La sucesión está acotada únicamente inferiormente
La sucesión no está acotada.
|