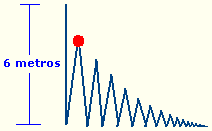
1. Se suelta una pelota desde una altura de 6 m. y empieza a botar
alcanzando en cada bote 3/4 de la altura del bote anterior. Hallar la
distancia total que recorrerá la bola hasta que deje de botar.
distancia = 24 metros
distancia = 35 metros
distancia = 42 metros
distancia = 40 metros
|
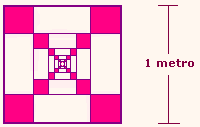
2. Hallar la porción sombreada de área del cuadrado de lado 1
metro, si se continúa sombreando indefinidamente, según indica la figura.
Tener en cuenta que cada lado de un cuadrado sombreado es 1/4 del lado del
cuadrado en el que está situado de esquina.
Área sombreada =
1/3 metros
Área sombreada =
1/4 metros
Área sombreada =
2/7 metros
Área sombreada =
3/10 metros
|
3. Hallar la suma de todos los términos de la progresión
geométrica indefinida
2+
1
2
+
(
1
2
)
2
+
(
1
2
)
3
+
(
1
2
)
4
+...
S=4−
2
S=4+2⋅
2
S=5+
2
S=5−2⋅
2
|
4. Hallar la suma de los infinitos términos de las siguientes sucesiones, cuyos términos se suman con el signo indicado:
a) 3−1+
1
3
−
1
9
+
1
27
−...
b) 8+6+
9
2
+
27
8
+
81
32
+...
a) S = 9/4 ; b)
S = 32
a) S = 7/4 ;
b) S = 34
a) S = 17/8 ;
b) S = 40
a) S = 3/12 ; b) S =
32/3
|
5. Hallar la suma de los términos de la sucesión, que puede expresarse
así
∑
n=1
∞
[
(0'7)
n
+
(0'9)
n
]
=[
0'7+0'9
]+[
(0'7)
2
+
(0'9)
2
]+...
S = 27/4
S = 12
S = 41/4
S = 34/3
|
6. Expresar los siguientes números decimales periódicos como la suma
de una progresión geométrica indefinida y escribir dicha suma como cociente
de dos enteros
P=0'74
9
¯
; Q=0'2
15
¯
P = 4/5
; Q = 2/9
P = 29/39 ; Q =
3/14
P = 3/4 ; Q = 71/330
P = 6/7 ; Q = 25/97
|
7. Calcular la suma de las siguientes progresiones geométricas
indefinidas
a)
∑
n=0
∞
(0'9)
n
; b)
∑
n=0
∞
(−0'6)
n
; c)
∑
n=0
∞
3⋅
(
3
2
)
n
a) S = 12 ; b)
S = 9/16 ; c) S = 89
a) S = 10 ; b) S = 5/8 ; c) S =
+ ∞
a) S = 100/9 ; b) S = 4/3 ; c) S = 143
a) S = 9 ; b) S = 3/8 ; c) S =
+ ∞
|
8. La suma de los infinitos términos de una progresión geométrica
decreciente es 4. El segundo término es 1. Determina la progresión.
3
2
, 1 ,
2
3
,
4
9
,
8
27
, ...
3 , 1 ,
1
3
,
1
9
,
1
27
, ...
2 , 1 ,
1
2
,
1
4
,
1
8
, ...
1
2
, 1 , 2 , 4 , 8 , ...
|
9. Calcula el valor de la siguiente expresión, utilizando para ello
la suma de una progresión geométrica indefinida
x=
5⋅
5⋅
5⋅
5⋅⋅⋅
5
5
5
x=5
5/8
x=5
8/5
x=5
7/5
x=5
7/8
|
10. En un triángulo equilátero de lado 1 cm. se unen los puntos
medios de los lados y se obtiene otro triángulo equilátero en el que, a su
vez, se repite la operación anterior, y así indefinidamente.
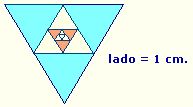
Calcula la suma de los perímetros de los infinitos triángulos que se
obtienen.
Suma de los perímetros = 12 cm.
Suma de los perímetros = 9 cm.
Suma de los perímetros = 8 cm.
Suma de los perímetros = 6 cm.
|