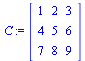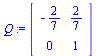Manipulación de matrices
Hay diversas formas de introducir una matriz en Maple. Por ejemplo, sin ánimo de ser exhaustivos
| > |
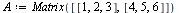 |
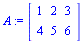 |
(1.1) |
o en modo habitual
| > |
 |
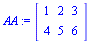 |
(1.2) |
| > |
 |
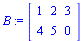 |
(1.3) |
El elemento que falta es interpretado como 0
Maple puede sumar matrices
| > |
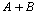 |
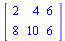 |
(1.4) |
Asimismo puede multiplicar matrices de tamaños adecuados
| > |
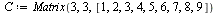 |
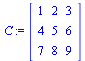 |
(1.5) |
| > |
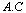 |
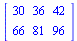 |
(1.6) |
Maple calcula el rango, pero necesita buscar la función en un paquete especial denominado Linear Algebra
| > |
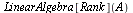 |
 |
(1.7) |
Maple calcula la traspuesta
| > |
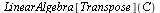 |
 |
(1.8) |
Si tenemos suficiente memoria podemos cargar de golpe el paquete
| > |
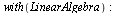 |
| > |
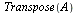 |
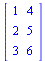 |
(1.9) |
| > |
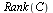 |
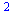 |
(1.10) |
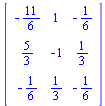
¿Qué menos que calcular la inversa de una matriz?
| > |
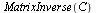 |
| Error, (in LinearAlgebra:-LA_Main:-MatrixInverse) singular matrix |
|
La matriz C no posee inversa. La modificamos un poco
| > |
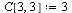 |
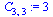 |
(1.11) |
| > |
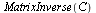 |
 |
(1.12) |
Y el determinante de una matriz cuadrada
| > |
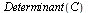 |
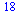 |
(1.13) |
Maple extrae submatrices; por ejemplo las filas 1, 3 y las columnas 1, 2 de C
| > |
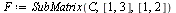 |
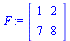 |
(1.14) |
Maple calcula valores y vectores propios de matrices cuadradas. Modificamos un poco F por claridad
| > |
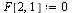 |
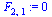 |
(1.15) |
| > |
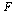 |
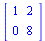 |
(1.16) |
| > |
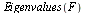 |
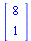 |
(1.17) |
| > |
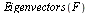 |
 |
(1.18) |
La respuesta de Maple son los valores propios y los vectores propios asociados a ellos.
Finalmente, Maple calcula -entre otras formas canónicas- la forma de Jordan
| > |
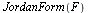 |
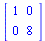 |
(1.19) |
Pudiendo evaluar la matriz de paso
| > |
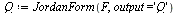 |
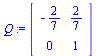 |
(1.20) |
En efecto,
| > |
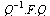 |
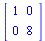 |
(1.21) |
Y muchas otras funciones más de Algebra Lineal que, en su momento, se verán.