RESOLUCIÓN DE INECUACIONES NO LINEALES
El tipo de inecuación y/o los conocimientos de quien aborda la resolución
aconsejarán seguir unas u otras pautas.
|
E
s
c
e
n
a
d
i
n
á
m
i
c
a
|
|
Una idea inicial sobre el conjunto
solución de una inecuación no lineal viene dada a través del applet que hay a la izquierda.
Modificando en la zona de control el valor de x, podemos observar que la inecuación
x−cos(x)≥0
tiene como conjunto solución un intervalo de la forma
(a,∞)
, donde a es aproximadamente 0.7.
El applet permite cambiar la expresión. Invitamos al lector a que introduzca en él las
expresiones que definen las inecuaciones mostradas a continuación, de las que puede ver una resolución detallada.
|
PRIMER EJEMPLO.
x
2
−1<0
x
2
−1<0⇔(x+1)(x−1)<0⇔{
x−1>0 ∧ x+1<0
∨
x−1<0 ∧ x+1>0
}⇔
⇔{
x>1 ∧ x<−1 → imposible
∨
x<1 ∧ x>−1 → −1<x<1
}⇒
Solución:
intervalo (−1,1)
|
SEGUNDO EJEMPLO.
1
2
<cos(x)≤1
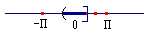
En la imagen sólo aparecen las soluciones de la inecuación comprendidas entre -
Π
y
Π
. A ese intervalo hay que unir los
(
−
Π
3
+2kΠ,
Π
3
+2kΠ
]
con k
∈ℤ
|
TERCER EJEMPLO.
x
2
−4
≥| x |−5
1. Ha de tenerse:
x
2
−4≥0 ⇔ x∈(−∞,−2]∪[2,+∞)
.
2.
x
2
−4
≥| x |−5 ⇒
x
2
−4
+5≥| x | ⇒
⇒ (x
2
−4)+25+10
x
2
−4
≥x
2
⇒
⇒
x
2
−4
≥−
21
10
3. Lo obtenido en 2. es cierto para todo valor determinado en 1. El conjunto solución es pues
(−∞,−2]∪[2,+∞)
|
CUARTO EJEMPLO.
|
x−1
x+2
|≤4
|
x−1
x+2
|≤4 ⇔ −4≤
x−1
x+2
≤4 ⇔
⇔{
−4(x+2)≤x−1≤4(x+2) si x+2>0→a
∨
−4(x+2)≥x−1≥4(x+2) si x+2<0→b
Caso
a
Caso
b
Solución:
(
−∞,−3
]∪[
−
7
5
,+∞
)
|
|
Maple :
Instrucciones para la resolución de inecuaciones |
