Forma reducida o forma canónica de una ecuación general de segundo grado
Los ejemplos y explicaciones anteriores sobre las cónicas reales se han basado en ecuaciones sencillas. Esto no significa, como ha quedado
implícito, que una ecuación general
ax
2
+by
2
+cxy+dx+ey+f=0
represente una curva más complicada.
Si se elige un sistema de coordenadas conveniente, una ecuación del tipo anterior puede siempre reducirse
a una de las formas canónicas dadas a continuación.
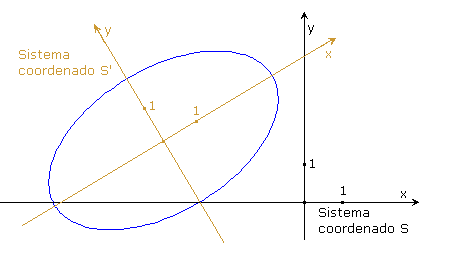
En la figura derecha, a título de ejemplo, aparece una elipse que respecto del sistema de coordenadas S tiene ecuación
0,55
x
2
+0,91
y
2
−0,66xy+5,17x−5,40y+10=0
La ecuación reducida es
x
2
3,33
2
+
y
2
1,89
2
=1
que se correspondería con la que dicha elipse tiene respecto del sistema coordenado S'.
|
|
|
FORMAS CANÓNICAS
|
x
2
a
2
+
y
2
b
2
−1=0 → Elipse
|
x
2
a
2
+
y
2
b
2
+1=0 → Elipse imaginaria
|
x
2
a
2
+
y
2
b
2
=0 → Punto
|
x
2
a
2
−
y
2
b
2
−1=0 → Hipérbola
|
x
2
a
2
−
y
2
b
2
=0 → Para de rectas secantes
|
y
2
−2px=0 → Parábola
|
x
2
−
a
2
=0 → Par de rectas paralelas
|
x
2
+
a
2
=0 → Par de rectas imaginarias
|
x
2
=0 → Par de rectas coincidentes
|
