PRINCIPIO ADITIVO
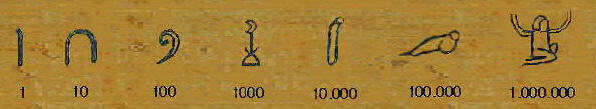 EJEMPLO
EJEMPLO
Un sistema de numeración se dice que sigue
un principio aditivo si se repiten los signos de
cada valor tantas veces como ese valor esté contenido en el número; se pueden escribir en
cualquier orden o disposición.
Un ejemplo de sistema que
utilizaba dicho criterio es el egipcio.
Al ser indiferente el
orden de los signos, estos se escribían a veces según criterios estéticos, y solían ir
acompañados de los jeroglíficos correspondientes al tipo de objeto
(animales, prisioneros, vasijas etc.) cuyo número indicaban.
En la figura
aparece el 276 tal y como figura en una estela en Karnak.
|
PRINCIPIO MULTIPLICATIVO

|
Se utiliza una combinación de dos signos, el
primero de menor valor que el segundo de forma que el menor indica el
número de veces que se considera el segundo.
Ejemplo el sistema chino.
Este principio se presenta
en combinación con el aditivo y en él es importante el orden de los
signos.
|
PRINCIPIO DEL VALOR POSICIONAL
El valor del signo depende del lugar que
ocupa. El orden de escritura es por tanto fundamental.
A la derecha se muestran unos ejemplos de lo que esto significa sobre nuestro actual sistema decimal.
Es fundamental la
existencia del cero (0) para indicar la ausencia de unidades de un cierto
orden. |
234 = 2·100 + 3·10 + 4 |
2304 = 2·1000 + 3·100 + 4 |
2340 = 2·1000 + 3·100 + 4·10 |
|
En general, si
N=
d
n
⋯
d
1
d
0
,
d
−1
⋯
d
−k
|
es un número expresado en el sistema decimal, su valor se corresponde con
N=
d
n
· 10
n
+⋯+
d
1
· 10
1
+
d
0
· 10
0
+
d
−1
· 10
−1
+⋯+
d
−k
· 10
−k
=
∑
i=−k
n
d
i
· 10
i
|
|
|
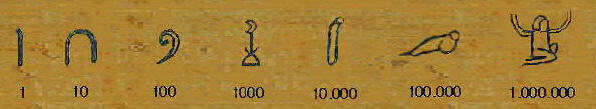 EJEMPLO
EJEMPLO
