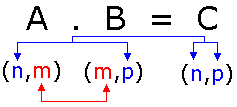Podemos introducir el producto de matrices en dos fases:
-
El producto de una matriz fila de dimensión (1,n) por una
matriz columna de dimensión (n,1) es una matriz de dimensión (1,1)
que se obtiene multiplicando cada término de la primera por cada
uno de la segunda y sumando así:
Se dice producto de la fila por la columna.
|
(
a
1
⋯
a
n
) · (
b
1
⋮
b
n
)
=
a
1
·
b
1
+⋯+
a
n
·
b
n
|
EJEMPLO
(
2
−3
4
)·(
1
2
−2
)=2·1−3·2+4·(−2)=−12
|
-
Dadas dos matrices A y B, si las filas de A
tienen la misma cantidad de términos que las columnas de B, podemos multiplicar
cada
fila de A por cada columna de B obteniendo una nueva matriz C, que se
dice matriz producto de A y B. Por ejemplo:
|
EJEMPLO
A=(
1
2
2
4
1
3
) B=(
3
1
0
1
2
2
)
⇓
C=(
(
1
2
)(
3
1
)
(
1
2
)(
1
2
)
(
1
2
)(
0
2
)
(
2
4
)(
3
1
)
(
2
4
)(
1
2
)
(
2
4
)(
0
2
)
(
1
3
)(
3
1
)
(
1
3
)(
1
2
)
(
1
3
)(
0
2
)
)=(
5
5
4
10
10
8
6
7
6
)
MathType@MTEF@5@5@+=feaafeart1ev1aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaOaaaeaacaaIYaaaleqaaaaa@36C4@
|
|