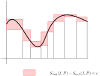
Gracias a las propiedades de las sumas superiores e inferiores podemos definir
|
Integral Inferior de f en [a,b] es el supremo de las
sumas inferiores de f, al considerar todas las posibles particiones de [a,b] |
|
Integral Superior de f en [a,b] es el ínfimo de las sumas superiores de
f, al considerar todas las posibles particiones de [a,b] |
y las funciones integrables:
|
Sea f una función acotada en un intervalo [a,b]. Se dice
que f es integrable si la integral inferior y la integral superior de f
en [a,b] coinciden. En ese caso, a ese número se le denomina integral de
f en [a,b], y se escribe |
El siguiente Teorema nos da un criterio para saber si una función es integrable o no, sin necesidad de calcular el valor de la integral:
|
Criterio de Integrabilidad de Riemann:
|