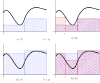
Sumas superiores e inferiores: propiedades


Para formalizar la idea de que las sumas superiores e inferiores de una función definidas por particiones del intervalo tiendan a un mismo número, necesitamos entender primero cómo varía el valor de estas sumas al cambiar la partición del intervalo. Hay que observar en primer lugar que las particiones no están ordenadas de una forma tan sencilla como las sucesiones: podemos tener particiones con más o menos cantidad de puntos, seleccionados en distintos lugares del intervalo.

Por ejemplo, en el intervalo [0,1] podemos definir las particiones P={ 0, 1 2 ,1 }   y   Q={ 0, 1 4 , 3 4 ,1 }, y no podemos decir que una sea menor o mayor que la otra, aunque Q tenga más puntos que P.

La forma de establecer un orden entre las particiones es la siguiente: dadas dos particiones P y Q de un intervalo [a,b], diremos que P es mayor o igual que Q si Q está contenida en P, y escribiremos Q≤P . De esta forma, aunque dos particiones sean incomparables, siempre se puede construir una tercera que sea mayor que las dos, uniendo los puntos de ambas: en nuestro ejemplo, S={ 0, 1 4 , 1 2 , 3 4 ,1 }.

Llamamos partición trivial a la más pequeña que puede haber en un intervalo, formada sólo por sus extremos P 0 ={ a,b }

Consideraremos f una función acotada definida en el intervalo [a,b]. Llamamos

m=inf⁡{ f(x),a≤x≤b }              M=sup⁡{ f(x),a≤x≤b }

Las sumas superiores e inferiores de una función acotada tienen las siguientes propiedades:

Propiedad 1:

Para cualquier partición P, la suma inferior es menor que la superior:

S inf⁡ (f,P)≤ S sup⁡ (f,P)

 

Propiedad 2:

Las sumas inferiores aumentan al aumentar el número de puntos de la partición, y las sumas superiores disminuyen:

Si P y Q son dos particiones, y P≤Q , entonces  S inf⁡ (f,P)≤ S inf⁡ (f,Q) y S sup⁡ (f,P)≥ S sup⁡ (f,Q)

Propiedad 3:

Una suma inferior es siempre menor que cualquier suma superior: Si P y Q son dos particiones cualesquiera, S inf⁡ (f,P)≤ S sup⁡ (f,Q)

 

Propiedad 4: 

Las sumas superiores e inferiores están acotadas superior e inferiormente: Para cualquier partición P se tiene m(b−a)≤ S inf⁡ (f,P)≤ S sup⁡ (f,P)≤M(b−a)