|
La diferencial de una función |
|
Cuando veamos el método de integración con cambios de variable, será necesario calcular diferenciales. Por eso explicamos ahora brevemente como se opera con diferenciales.
|
|
Se llama diferencial de f(x) en el punto x a la siguiente expresión:
|
|
df(x)=f'(x)dx
MathType@MTEF@5@5@+=feaafiart1ev1aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamizaiaadAgacaGGOaGaamiEaiaacMcacqGH9aqpcaWGMbGaai4jaiaacIcacaWG4bGaaiykaiaadsgacaWG4baaaa@40F0@
|
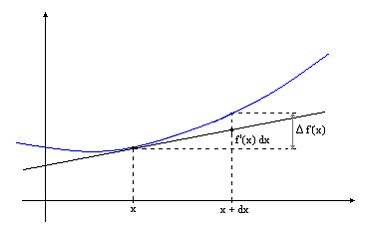 |
La diferencial es una aproximación de la variación
de f(x) cuando la variable x se incrementa en dx:
|
|
Δf(x)=f(x+dx)−f(x)≈df(x)
MathType@MTEF@5@5@+=feaafiart1ev1aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeuiLdqKaamOzaiaacIcacaWG4bGaaiykaiabg2da9iaadAgacaGGOaGaamiEaiabgUcaRiaadsgacaWG4bGaaiykaiabgkHiTiaadAgacaGGOaGaamiEaiaacMcacqGHijYUcaWGKbGaamOzaiaacIcacaWG4bGaaiykaaaa@4BAD@
|
pues la pendiente de la recta tangente a la gráfica en
el punto x es
f'(x)
MathType@MTEF@5@5@+=feaafiart1ev1aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamOzaiaacEcacaGGOaGaamiEaiaacMcaaaa@39DA@
.
|
| Ejemplos |
|
d(
e
3x
)=3
e
3x
dx
MathType@MTEF@5@5@+=feaafiart1ev1aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamizaiaacIcacaWGLbWaaWbaaSqabeaacaaIZaGaamiEaaaakiaacMcacqGH9aqpcaaIZaGaamyzamaaCaaaleqabaGaaG4maiaadIhaaaGccaWGKbGaamiEaaaa@418F@
|
|
d(ln(4
x
2
+3))=
8x
4
x
2
+3
dx
MathType@MTEF@5@5@+=feaafiart1ev1aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaqcaaQaamizaiaacIcaciGGSbGaaiOBaiaacIcacaaI0aGaamiEaOWaaWbaaSqabeaacaaIYaaaaOGaey4kaSIaaG4maiaacMcacaGGPaGaeyypa0ZaaSaaaeaacaaI4aGaamiEaaqaaiaaisdacaWG4bWaaWbaaSqabeaacaaIYaaaaOGaey4kaSIaaG4maaaacaWGKbGaamiEaaaa@4975@
|
