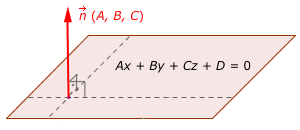Un plano, p,
queda determinado, según lo visto en el apartado anterior, cuando se conocen un punto,
P, y dos vectores
u→
y v→
MathType@MTEF@5@5@+=feaaguart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLw
BLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc
9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGabmyDayaalaG
aaeiiaiaabccacaqG5bGaaeiiaiaabccaceWG2bGbaSaaaaa@3B93@
paralelos al mismo (vectores de dirección o vectores directores).
Hay una forma, aún más sencilla, de determinar un plano. Con un punto del plano y un vector perpendicular al
mismo, el plano queda perfectamente determinado.
Se llama VECTOR NORMAL del plano a cualquier
vector perpendicular al mismo.
Además,
VECTOR NORMAL DEL PLANO
Si Ax + By +Cz + D = 0 es la ecuación general (implícita) de un plano,
n→
=( A,
B,
C )
MathType@MTEF@5@5@+=feaagu
art1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gB
aerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0x
e9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqa
aeGaciGaaiaabeqaamaabaabaaGcbaWaa8HaaeaacaWGUbaacaGLxdcacqGH9aqpdaqadaqaai
aadgeacaGGSaGaaGjbVlaadkeacaGGSaGaaGjbVlaadoeaaiaawIcacaGLPaaaaaa@41F7@
es un vector normal del plano.
|
Efectivamente, si se toman dos puntos arbitrarios, P(x0, y
0,
z0) y X(x, y, z) del plano
π:
Ax
+By+Cz+
D=0
MathType@MTEF@5@5@+=feaaguart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9
gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9
pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeqiWdaNaaiOoai
aadgeacaWG4bGaey4kaSIaamOqaiaadMhacqGHRaWkcaWGdbGaamOEaiabgUcaRiaadseacqGH9aqpcaaIWaaaaa@42EB@
(ver figura), se tiene que las coordenadas de ambos puntos
satisfacen la ecuación del plano:
Ax
+By+Cz+
D=0 A
x0 +By0
+Cz0 +
D=0
restando las igualdades: A
( x−x0
)+B(
y−y0
)+C( z
−z0 )
=0
que se puede expresar como un producto escalar:
( A,
B, C
)⋅( x
−x0 ,
y−y0
, z−
z0 )=0
resultando:
n→ ⋅
PX
→ =0
;
n→
⊥ PX
→
;
n →
⊥π
MathType@MTEF@5@5@+=feaaguart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gB
aerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9
Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGceaqabeaacaWGbbGaamiEaiab
gUcaRiaadkeacaWG5bGaey4kaSIaam4qaiaadQhacqGHRaWkcaWGebGaeyypa0JaaGimaaqaaiaadgeacaWG4bWaaSbaaSqaaiaa
icdaaeqaaOGaey4kaSIaamOqaiaadMhadaWgaaWcbaGaaGimaaqabaGccqGHRaWkcaWGdbGaamOEamaaBaaaleaacaaIWaaabeaa
kiabgUcaRiaadseacqGH9aqpcaaIWaaabaGaaeOCaiaabwgacaqGZbGaaeiDaiaabggacaqGUbGaaeizaiaab+gacaqGGaGaaeiB
aiaabggacaqGZbGaaeiiaiaabMgacaqGNbGaaeyDaiaabggacaqGSbGaaeizaiaabggacaqGKbGaaeyzaiaabohacaqG6aaabaGa
amyqamaabmaabaGaamiEaiabgkHiTiaadIhadaWgaaWcbaGaaGimaaqabaaakiaawIcacaGLPaaacqGHRaWkcaWGcbWaaeWaaeaa
caWG5bGaeyOeI0IaamyEamaaBaaaleaacaaIWaaabeaaaOGaayjkaiaawMcaaiabgUcaRiaadoeadaqadaqaaiaadQhacqGHsisl
caWG6bWaaSbaaSqaaiaaicdaaeqaaaGccaGLOaGaayzkaaGaeyypa0JaaGimaaqaaiaabghacaqG1bGaaeyzaiaabccacaqGZbGa
aeyzaiaabccacaqGWbGaaeyDaiaabwgacaqGKbGaaeyzaiaabccacaqGLbGaaeiEaiaabchacaqGYbGaaeyzaiaabohacaqGHbGa
aeOCaiaabccacaqGJbGaae4Baiaab2gacaqGVbGaaeiiaiaabwhacaqGUbGaaeiiaiaabchacaqGYbGaae4BaiaabsgacaqG1bGa
ae4yaiaabshacaqGVbGaaeiiaiaabwgacaqGZbGaae4yaiaabggacaqGSbGaaeyyaiaabkhacaqG6aaabaWaaeWaaeaacaWGbbGa
aiilaiaaysW7caWGcbGaaiilaiaaysW7caWGdbaacaGLOaGaayzkaaGaeyyXIC9aaeWaaeaacaWG4bGaeyOeI0IaamiEamaaBaaa
leaacaaIWaaabeaakiaacYcacaaMe8UaamyEaiabgkHiTiaadMhadaWgaaWcbaGaaGimaaqabaGccaGGSaGaaGjbVlaadQhacqGH
sislcaWG6bWaaSbaaSqaaiaaicdaaeqaaaGccaGLOaGaayzkaaGaeyypa0JaaGimaaqaaiaabkhacaqGLbGaae4CaiaabwhacaqG
SbGaaeiDaiaabggacaqGUbGaaeizaiaab+gacaqG6aaabaGabmOBayaalaGaeyyXIC9aa8HaaeaacaWGqbGaamiwaaGaay51GaGa
eyypa0JaaGimaiaaysW7caaMe8Uaai4oaiaaysW7caaMe8UabmOBayaalaGaeyyPI41aa8HaaeaacaWGqbGaamiwaaGaay51GaGa
aGjbVlaaysW7caGG7aGaaGjbVpaaL4babaGaaGjbVlqad6gagaWcaiabgwQiEjabec8aWjaaysW7aaaaaaa@EDAC@
Ello permite, por último, obtener de una forma muy rápida la ecuación de un plano conocido un vector
normal (perpendicular), (A, B, C) y un punto
P(x0, y0,
z0) :
ECUACIÓN DEL PLANO CONOCIDOS UN VECTOR NORMAL Y UN PUNTO
p: A
(x − x0) +
B(y − y0) +
C(z − z0) = 0
|
|
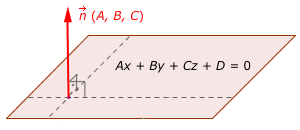
Vector normal del plano
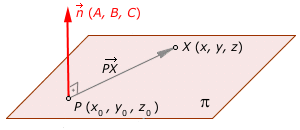
El vector normal del plano es perpendicular
a cualquier vector
PX
→
MathType@MTEF@5@5@+=feaaguart1ev2aaatCvAUfeBSjuyZL2y
d9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0
Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr
=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaa8HaaeaacaWGqbGaamiwaaGaay51Gaaaaa@3958@
del plano.
|
|
También es posible emplear los vectores normales de los planos que determinan una recta
cuando viene dada en forma implícita, esto es, como intersección de dos planos. El vector
de dirección de la recta se puede obtener, entonces, mediante el producto vectorial de
los vectores normales de los planos (ver figura).
r
:{ A
x+By+C
z+D=0
A ′x+
B ′y+ C
′z+ D
′=0
u→
= n →
1 ×
n →2 =
( A, B
, C )
×( A′
, B′
, C′
)
MathType@MTEF@5@5@+=feaaguart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI
9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpC0xe9LqFHe9Lqpepeea0df9q8
as0=LqLs=Jirpepeea0=as0Fb9pgea0lrP0xe9Fve9Fve9qapdbaqaaeGaciGaaiaabeqaamaabaabaaGceaqabeaacaWGYbG
aaiOoamaaceaaeaqabeaacaWGbbGaamiEaiabgUcaRiaadkeacaWG5bGaey4kaSIaam4qaiaadQhacqGHRaWkcaWGebGaeyyp
a0JaaGimaaqaaiqadgeagaqbaiaadIhacqGHRaWkceWGcbGbauaacaWG5bGaey4kaSIabm4qayaafaGaamOEaiabgUcaRiqad
seagaqbaiabg2da9iaaicdaaaGaay5EaaaabaGabmyDayaalaGaeyypa0JabmOBayaalaWaaSbaaSqaaiaaigdaaeqaaOGaey
41aqRabmOBayaalaWaaSbaaSqaaiaaikdaaeqaaOGaeyypa0ZaaeWaaeaacaWGbbGaaiilaiaaysW7caWGcbGaaiilaiaaysW
7caWGdbaacaGLOaGaayzkaaGaey41aq7aaeWaaeaaceWGbbGbauaacaGGSaGaaGjbVlqadkeagaqbaiaacYcacaaMe8Uabm4q
ayaafaaacaGLOaGaayzkaaaaaaa@6C9E@
|

Vector dirección de la recta intersección de dos planos
|