En los apartados anteriores has visto dos operaciones entre vectores (producto por un número y suma de vectores); en ambos casos el resultado de la operación era un nuevo vector. A continuación se introducirá una nueva operación entre vectores cuyo resultado no es un vector sino un número, un "escalar".

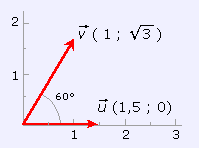
El resultado de multiplicar escalarmente dos vectores es un número que se obtiene multiplicando los módulos por el coseno del ángulo que forman ambos vectores.

(Cuando en un mismo contexto o situación se emplean a la vez vectores y números es común referirse a estos últimos como "escalares" para distinguirlos de los vectores).

En el ejemplo de la figura se han representado dos vectores referidos a una base ortonormal y se calcula su producto escalar:

  | u → |=1,5 | v → |= 1 2 + ( 3 ) 2 =2  (teorema de Pitágoras) u → ⋅ v → =| u → |⋅| v → |cos⁡( u → , v → )=1,5⋅2⋅cos⁡60º=3 1 2 = 3 2

Como puedes apreciar, el producto escalar es un número que es máximo cuando ambos vectores coinciden en dirección y sentido ( α=0º;​​ cos⁡0º=1 ), vale cero cuando son perpendiculares ( α=90º;​​ cos⁡90º=0 ), y es mínimo cuando tienen direcciones opuestas ( α=180º;​​ cos⁡180º=-1 ). Se exponen, en la siguiente página, las propiedades de esta operación.