Geometría Analítica I 6

Combinación lineal de vectores


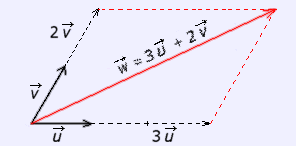
Acabas de ver en el apartado anterior la forma en que se suman dos vectores y cómo se puede multiplicar un número por un vector. Es posible, como en el ejemplo de la figura, representar el resultado de realizar de manera consecutiva ambas operaciones sobre una pareja de vectores. Se ha obtenido, así, un nuevo vector w→ =3 u→ + 2 v→ Se dice, entonces, que w → es COMBINACIÓN LINEAL de u → y v → .

Y, en general:

Un vector w→ es COMBINACIÓN LINEAL de u→ y v→ si existen números a y b tales que:

w→ =a u→ + b v→

O, de forma aún más general:

Un vector w→ es COMBINACIÓN LINEAL de u →1 , u →2 , ... u →n si existen números a1 , a2 , ... an tales que:

w→ = a1 u →1 + a2 u →2 + ... + an u →n


En la figura de la derecha tienes representada una combinación lineal de cuatro vectores. w→ = 2 u →1 + u →2 + 2,5 u →3 + 1,5 u →4

¡CUIDADO con el lenguaje! Pincha en el icono de la ventana para aclarar el correcto uso de la expresión "combinación lineal". ¿Qué características tienen las combinaciones lineales de un solo vector, de dos vectores, de tres, ... ?

	Si se toman dos vectores, a → y b → , distintos de cero y no paralelos, cualquier otro vector u → se puede escribir como combinación lineal de a → y b → . Esto puedes comprobarlo en la escena de la izquierda. Al "pinchar y arrastrar" sobre el punto P se van dibujando distintos vectores u → , a la vez que aparece el paralelogramo de direcciones a → y b → que permite escribir u → como combinación lineal de a → y b → . 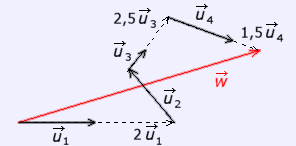Los datos de la combinación se escriben en la parte superior del cuadro: u→ =λ1 a→ +λ2 b→ Además, para cada vector u → la combinación lineal es única, es decir, los coeficientes λ1 y λ2 son únicos. ("λ " : undécima letra del alfabeto griego de nombre lambda; se corresponde con la "ele" del alfabeto latino; su mayúscula es "Λ" )

	En esta otra escena de la izquierda se intenta hacer lo mismo con tres vectores, a→ , b→ y c→ (azul, verde y rosa) que están "anclados" y no se pueden modificar. Hay, además, otro vector, u→ (blanco con borde negro), que permanece, igualmente, "fijo". Si "pinchas" sobre el punto P y lo deslizas horizontalmente aparece el vector u→ como combinación lineal de a→ , b→ y c→ (El punto P solo puede moverse horizontalmente, pues se encuentra "ligado" a la dirección que le impone el vector a→ ) Los datos de la combinación se escriben en la parte superior del cuadro: u → = λ 1 a → + λ 2 b → + λ 3 c → (Para realizar esa suma se ha empleado la "regla del triángulo") Puedes, de esta forma, comprobar cómo hay infinitas formas de combinar linealmente a → , b → y c → para dar lugar a un mismo vector u → . Fíjate como los vectores del mismo color (azul, verde, rosa) permanecen siempre paralelos en una dirección que no se modifica cuando deslizas el punto P.
	¿Y cómo son, por último, las combinaciones lineales de un solo vector? En la escena de la izquierda puedes observar como son las combinaciones lineales del vector a → . "Pinchando y arrastrando" sobre el punto P van apareciendo los distintos vectores u → , que se pueden formar. Los datos de la combinación lineal se escriben en la parte superior del cuadro: u → =λ a → El conjunto de todos esos vectores, que son combinación lineal de a → , se denomina recta vectorial.

En conclusión:

Un solo vector (no nulo) genera, mediante combinaciones lineales, toda una recta vectorial.

Dos vectores (no nulos y no paralelos) generan, mediante combinaciones lineales, todos los vectores del plano. Además, en este caso, cada vector se obtiene mediante una combinación lineal única.

Tres o más vectores (no nulos y no paralelos) generan, mediante combinaciones lineales, todos los vectores del plano. En este caso, cada vector se puede obtener mediante infinitas combinaciones lineales.