Y la suma, ¿tendrá algún significado la suma de vectores?

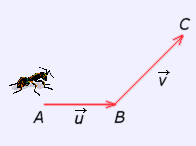
La hormiga "Figa" desea trasladarse de A hacia B mediante el vector  u →   , y desde allí al punto C mediante el vector  v →   . ¿Habrá algún vector con el que pueda desplazarse directamente desde A hasta C?

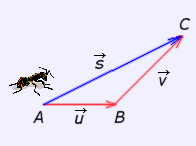
Hay, efectivamente, un vector,  s →   , que le permitiría ir directamente desde A hasta C. A este vector se le llama vector suma de  u →   y  v → .

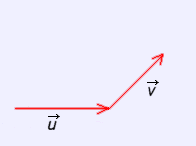
Los pasos a dar para obtener el vector suma son:

1. Tomar un representante de uno de ellos (  v →   por ejemplo) que tenga por origen el extremo del otro (  u →   en este caso).

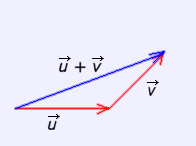
2. Formar el vector suma uniendo el origen del primero con el extremo del segundo.

Este procedimiento empleado para obtener la suma se denomina "REGLA DEL TRIÁNGULO"

Suma de vectores ("regla del triángulo")

Hay otra forma de sumar los vectores:

1. Tomar representantes de ambos vectores que tengan el mismo origen.

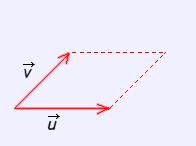
2. Trazar paralelas para formar el paralelogramo determinado por los vectores.

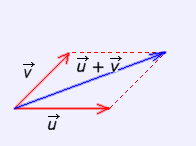
3. Formar el vector suma uniendo el origen común con el extremo de la diagonal que parte de ese mismo punto.

Este método empleado para obtener la suma se denomina "REGLA DEL PARALELOGRAMO".

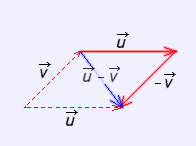
Suma de vectores ("regla del paralelogramo")

En la escena de la izquierda puedes apreciar cómo se realiza la suma empleando la "regla del paralelogramo".

Además, y como puedes observar en la figura de la derecha, la RESTA de los vectores viene dada por la otra diagonal del paralelogramo.

Ten en cuenta que para restar  u → − v →   habrás de sumar  u →   con el opuesto de  v →   .

u → − v → = u → +( − v → )

Resta de vectores