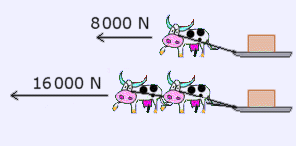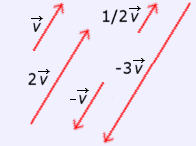Operaciones con vectores. Producto por un número
|
¿Por qué o para qué operar con vectores? Recuerda que el objetivo de la geometría analítica era sustituir los objetos propios del plano geométrico (puntos, rectas, ...) por otros propios del álgebra como expresiones, números o ecuaciones. Está claro que los puntos no se pueden sumar o multiplicar y, en cambio, verás enseguida cómo con los vectores puedes efectuar algunas operaciones. |
|
|
PRODUCTO DE UN NÚMERO POR UN VECTOR ¿Qué significado se podrá adjudicar al producto de un número por un vector? |
|
|
Si en un concurso de arrastre una vaca es capaz de aportar un vector fuerza de 8 000 N en la dirección horizontal, dos vacas de las mismas características proporcionarán otro vector con la misma dirección y sentido, y con una intensidad o módulo que será el doble, esto es, de 16 000 N.
|
|
|
Podemos así definir: | |
|
el PRODUCTO de un número k,
por un vector
Módulo: es el producto del valor
absoluto de k por el módulo de
Dirección: la misma que
Sentido: el mismo que
|
|
|
|
|
|
|
|
vector cero: el producto
vector opuesto: el producto
|