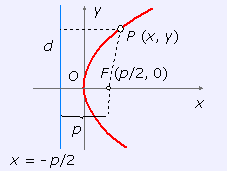Se llama así, ecuación reducida, a la que se obtiene tomando como origen de coordenadas el vértice de la parábola y como eje de abscisas el eje de simetría de la parábola. El foco aparece así situado en (p/2, 0) y la ecuación de la directriz resulta ser x = - p/2 .
d (P, F) = d (P, d)
sustituyendo en las fórmulas que calculan la distancia entre dos puntos y la distancia de un punto a una recta:
(
x−
p
2
)
2
+
y
2
=x+
p
2
MathType@MTEF@5@5@+=feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqipu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaOaaaeaadaqadaqaaiaadIhacqGHsisldaWcaaqaaiaadchaaeaacaaIYaaaaaGaayjkaiaawMcaamaaCaaaleqabaGaaGOmaaaakiabgUcaRiaadMhadaahaaWcbeqaaiaaikdaaaaabeaakiabg2da9iaadIhacqGHRaWkdaWcaaqaaiaadchaaeaacaaIYaaaaaaa@437D@
elevando al cuadrado ambos miembros y simplificando:
|