La distancia entre dos puntos P (x₁, y₁) y Q (x₂, y₂) viene dada por el módulo del vector PQ → MathType@MTEF@5@5@+=feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqipu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaa8HaaeaacaWGqbGaamyuaaGaay51Gaaaaa@392C@   que une ambos puntos.

d(P,Q)=| PQ → |= ( x 2 − x 1 ) 2 + ( y 2 − y 1 ) 2 MathType@MTEF@5@5@+=feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqipu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamizaiaacIcacaWGqbGaaiilaiaadgfacaGGPaGaeyypa0ZaaqWaaeaadaWhcaqaaiaadcfacaWGrbaacaGLxdcaaiaawEa7caGLiWoacqGH9aqpdaGcaaqaaiaacIcacaWG4bWaaSbaaSqaaiaaikdaaeqaaOGaeyOeI0IaamiEamaaBaaaleaacaaIXaaabeaakiaacMcadaahaaWcbeqaaiaaikdaaaGccqGHRaWkcaGGOaGaamyEamaaBaaaleaacaaIYaaabeaakiabgkHiTiaadMhadaWgaaWcbaGaaGymaaqabaGccaGGPaWaaWbaaSqabeaacaaIYaaaaaqabaaaaa@520D@

La distancia de un punto P (x₀, y₀) a una recta r: A x + B y + C = 0  es la menor de las distancias entre P y los puntos de la recta, y viene dada por la expresión:

d (P, r)= | A x 0 +B y 0 +C | A 2 + B 2 MathType@MTEF@5@5@+=feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqipu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamizaiaaysW7caGGOaGaamiuaiaacYcacaaMe8UaamOCaiaacMcacqGH9aqpdaWcaaqaaiaacYhacaWGbbGaamiEamaaBaaaleaacaaIWaaabeaakiabgUcaRiaadkeacaWG5bWaaSbaaSqaaiaaicdaaeqaaOGaey4kaSIaam4qaiaacYhaaeaadaGcaaqaaiaadgeadaahaaWcbeqaaiaaikdaaaGccqGHRaWkcaWGcbWaaWbaaSqabeaacaaIYaaaaaqabaaaaaaa@4D0A@

(Pincha    en el icono de la ventana para mostrar el origen de la expresión)

Otro método, sin necesidad de usar fórmula alguna, consiste en:

1.  Obtener la ecuación de la recta t perpendicular a r que pasa por P.

2.  Resolver el sistema formado por ambas rectas obteniendo así el punto H.

3.  d (P, r) = d (P, H).

Si, por último, se desea calcular la distancia entre dos rectas paralelas -en cualquier otro caso su distancia es cero- no hay más que tomar un punto cualquiera de una de las rectas y calcular la distancia de ese punto a la otra recta.

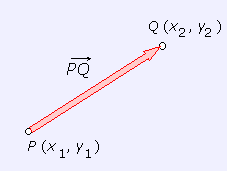
distancia entre dos puntos

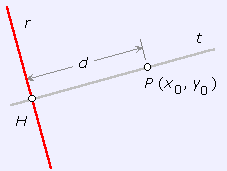
distancia del punto P a la recta r