Si en las ecuaciones paramétricas
se despeja t en ambas ecuaciones y se iguala
quitando, por último, denominadores y pasando todo al primer miembro
queda, en definitiva:
ECUACIÓN GENERAL O IMPLÍCITA DE LA RECTA Ax + By + C = 0 |
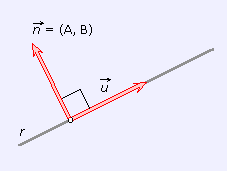
Al
vector ![]()
De forma recíproca el conocimiento de un vector normal de una recta resulta de gran utilidad para la obtención de su ecuación general, pues proporciona de forma directa los coeficientes A y B de dicha ecuación.