Geometría Analítica I 16

Ecuaciones de la recta

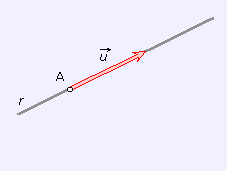
Una recta r queda determinada conociendo un punto, A , y un vector , u →  , paralelo a la recta (vector direccción).

¿Qué condición debe cumplir un punto genérico, X , para que pertenezca a la recta?

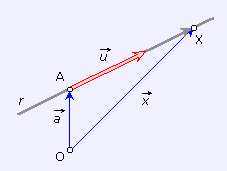
La condición es que los vectores  AX →   y   u →   sean paralelos, proporcionales, combinación lineal el uno del otro. Existirá, así, un número, t , tal que:

  AX → = t  u →

Según la "regla del triángulo" (ver figura):  x → = a → + AX →

Y, en definitiva:

ECUACIÓN VECTORIAL DE LA RECTA

x → = a → +t  u →  

Sustituyendo los vectores por sus coordenadas:

( x, y )=( a 1  , a 2 )+t ( u 1  , u 2 )

Y despejando:

ECUACIONES PARAMÉTRICAS DE LA RECTA

{ x= a 1 +t  u 1 y= a 2 +t  u 2