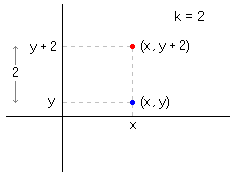Gráfica de  y = f(x) + k

Conocida la gráfica de  y = f(x), ¿cómo es la gráfica de  y = f(x) + k?

Si  (x, y)  es un punto de la gráfica de la primera función,  (x, y + k)  lo será de la segunda función. Así, para obtener la gráfica buscada no habrá más que desplazar k unidades hacia arriba (k>0) la gráfica de  f(x). Si k<0 el desplazamiento se hará hacia abajo.

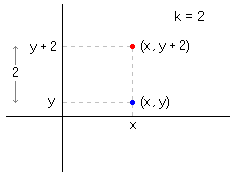
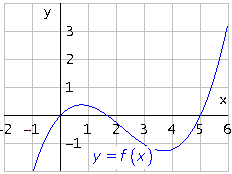
	En la escena de la izquierda pruebe a "pinchar y arrastrar" sobre el punto gris, desplazándolo verticalmente. Podrá comprobar cómo se modifica la gráfica (color rojo) a medida que cambia el valor de k.
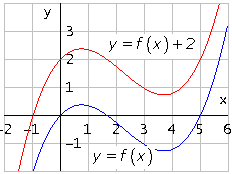
	A menudo puede resultar más cómodo desplazar el eje X k unidades hacia abajo (si k>0) o hacia arriba (si k<0). En definitiva, desplazar el eje X puede ser más fácil que desplazar la curva. En la escena de la izquierda pruebe a "pinchar y arrastrar" sobre el punto gris, desplazándolo verticalmente. Podrá comprobar cómo se modifican la gráfica y su ecuación a medida que cambia el valor de k. Para interpretar correctamente lo que ocurre tenga en cuenta que, en el ejemplo propuesto, k es la "ordenada en el origen" de la función.