Ramas infinitas

Las gráficas de las funciones presentan frecuentemente ramas que se alejan indefinidamente del origen, ramas infiinitas, para cuyo estudio se emplea como herramienta el cálculo de límites (en un punto o en el infinito).

Cuando una rama infinita se asemeja o se comporta como una recta, recibe el nombre de rama asíntótica, y la correspondiente recta se llama entonces asíntota.

En las gráficas de la derecha se muestran distintas ramas infinitas.

imagen:  de 

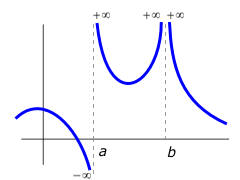
Asíntotas verticales

Son las que aparecen cuando, al obtener el límite de una función en un punto, este resulta infinito.

lim⁡ x→+/− a  f(x )=+/− ∞ MathType@MTEF@5@5@+=feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVC0de9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaCbeaeaaciGGSbGaaiyAaiaac2gaaSqaaiaadIhacqGHsgIRcqGHRaWkcaGGVaGaeyOeI0IaaGPaVlaadggaaeqaaOGaaGjbVlaadAgadaqadaqaaiaadIhaaiaawIcacaGLPaaacqGH9aqpcqGHRaWkcaGGVaGaeyOeI0IaaGPaVlabg6HiLcaa@4BE1@

En las funciones racionales,   f( x)= P( x) Q( x) MathType@MTEF@5@5@+=feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVC0de9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamOzamaabmaabaGaamiEaaGaayjkaiaawMcaaiabg2da9maalaaabaGaamiuamaabmaabaGaamiEaaGaayjkaiaawMcaaaqaaiaadgfadaqadaqaaiaadIhaaiaawIcacaGLPaaaaaaaaa@40AD@ , se pueden encontrar en los ceros del denominador (Q(x) = 0).

Para estudiar la posición de la curva respecto de la asíntota vertical no hay más que calcular los límites laterales   lim⁡ x→+/− a  f( x) MathType@MTEF@5@5@+=feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVC0de9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaCbeaeaaciGGSbGaaiyAaiaac2gaaSqaaiaadIhacqGHsgIRcqGHRaWkcaGGVaGaeyOeI0IaaGPaVlaadggaaeqaaOGaaGjbVlaadAgadaqadaqaaiaadIhaaiaawIcacaGLPaaaaaa@455D@ .

Asíntotas horizontales

Son las que aparecen cuando, al obtener el límite de una función en el infinito, este resulta finito.

lim⁡ x→+ ∞  f( x)=k MathType@MTEF@5@5@+=feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVC0de9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaCbeaeaaciGGSbGaaiyAaiaac2gaaSqaaiaadIhacqGHsgIRcqGHRaWkcaaMc8UaeyOhIukabeaakiaaysW7caWGMbWaaeWaaeaacaWG4baacaGLOaGaayzkaaGaeyypa0Jaam4Aaaaa@463E@

Las funciones racionales,   f( x)= P( x) Q( x) MathType@MTEF@5@5@+=feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVC0de9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamOzamaabmaabaGaamiEaaGaayjkaiaawMcaaiabg2da9maalaaabaGaamiuamaabmaabaGaamiEaaGaayjkaiaawMcaaaqaaiaadgfadaqadaqaaiaadIhaaiaawIcacaGLPaaaaaaaaa@40AD@ , tienen asíntotas horizontales cuando   grado P ≤ grado Q MathType@MTEF@5@5@+=feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVC0de9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaae4zaiaabkhacaqGHbGaaeizaiaab+gacaqGGaGaamiuaiaabccacqGHKjYOcaqGGaGaae4zaiaabkhacaqGHbGaaeizaiaab+gacaqGGaGaamyuaaaa@4493@ .

Para estudiar la posición de la curva respecto de la asíntota horizontal hay que analizar el signo de   f( x)−k  cuando  x≫0 MathType@MTEF@5@5@+=feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVC0de9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamOzamaabmaabaGaamiEaaGaayjkaiaawMcaaiabgkHiTiaadUgacaqGGaGaaeiiaiaabogacaqG1bGaaeyyaiaab6gacaqGKbGaae4BaiaabccacaqGGaGaamiEaiablUMi=iaaicdaaaa@45E9@ ; si este resulta positivo la curva se encuentra por encima de la asíntota y si es negativo lo hará por debajo.

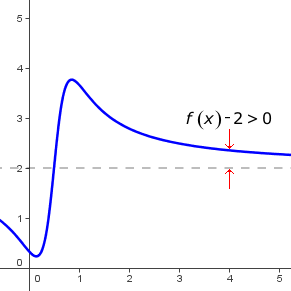
En el ejemplo de la gráfica,   f(x )= 16x2 −6x+1 8x2 −8x+3 MathType@MTEF@5@5@+=feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVC0de9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamOzamaabmaabaGaamiEaaGaayjkaiaawMcaaiabg2da9maalaaabaGaaGymaiaaiAdacaWG4bWaaWbaaSqabeaacaaIYaaaaOGaeyOeI0IaaGOnaiaadIhacqGHRaWkcaaIXaaabaGaaGioaiaadIhadaahaaWcbeqaaiaaikdaaaGccqGHsislcaaI4aGaamiEaiabgUcaRiaaiodaaaaaaa@48A5@ , la función tiene asíntota horizontal  y = 2, pues   lim⁡ x→∞    16x2 −6x+1 8x2 −8x+3 = 168 =2 MathType@MTEF@5@5@+=feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVC0de9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaCbeaeaaciGGSbGaaiyAaiaac2gaaSqaaiaadIhacqGHsgIRcqGHEisPaeqaaOGaaGjbVlaaykW7daWcaaqaaiaaigdacaaI2aGaamiEamaaCaaaleqabaGaaGOmaaaakiabgkHiTiaaiAdacaWG4bGaey4kaSIaaGymaaqaaiaaiIdacaWG4bWaaWbaaSqabeaacaaIYaaaaOGaeyOeI0IaaGioaiaadIhacqGHRaWkcaaIZaaaaiabg2da9maalaaabaGaaGymaiaaiAdaaeaacaaI4aaaaiabg2da9iaaikdaaaa@53C9@ .

Para averiguar si la curva, lejos del origen, se encuentra por encima o por debajo de la asíntota, se estudia el signo de la resta   f( x)−2= 16 x 2−6x+1 8 x 2−8x+3 −2= 16 x 2 −6x+1− 16 x 2 +16x−6 8 x 2−8x+3 = 10x−5 8 x 2−8x+3 MathType@MTEF@5@5@+=feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVC0de9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamOzamaabmaabaGaamiEaaGaayjkaiaawMcaaiabgkHiTiaaikdacqGH9aqpdaWcaaqaaiaaigdacaaI2aGaamiEamaaCaaaleqabaGaaGOmaaaakiabgkHiTiaaiAdacaWG4bGaey4kaSIaaGymaaqaaiaaiIdacaWG4bWaaWbaaSqabeaacaaIYaaaaOGaeyOeI0IaaGioaiaadIhacqGHRaWkcaaIZaaaaiabgkHiTiaaikdacqGH9aqpdaWcaaqaamaaKiaabaGaaGymaiaaiAdacaWG4bWaaWbaaSqabeaacaaIYaaaaaaakiabgkHiTiaaiAdacaWG4bGaey4kaSIaaGymaiabgkHiTmaaKiaabaGaaGymaiaaiAdacaWG4bWaaWbaaSqabeaacaaIYaaaaaaakiabgUcaRiaaigdacaaI2aGaamiEaiabgkHiTiaaiAdaaeaacaaI4aGaamiEamaaCaaaleqabaGaaGOmaaaakiabgkHiTiaaiIdacaWG4bGaey4kaSIaaG4maaaacqGH9aqpdaWcaaqaaiaaigdacaaIWaGaamiEaiabgkHiTiaaiwdaaeaacaaI4aGaamiEamaaCaaaleqabaGaaGOmaaaakiabgkHiTiaaiIdacaWG4bGaey4kaSIaaG4maaaaaaa@71A0@ , que, para valores   x≫0 MathType@MTEF@5@5@+=feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVC0de9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiEaiablUMi=iaaicdaaaa@3883@ , resulta   10x−5 8 x 2−8x+3 ≈ 10x 8 x 2 = 5 4x >0 MathType@MTEF@5@5@+=feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVC0de9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaSaaaeaacaaIXaGaaGimaiaadIhacqGHsislcaaI1aaabaGaaGioaiaadIhadaahaaWcbeqaaiaaikdaaaGccqGHsislcaaI4aGaamiEaiabgUcaRiaaiodaaaGaeyisIS7aaSaaaeaacaaIXaGaaGimaiaadIhaaeaacaaI4aGaamiEamaaCaaaleqabaGaaGOmaaaaaaGccqGH9aqpdaWcaaqaaiaaiwdaaeaacaaI0aGaamiEaaaacqGH+aGpcaaIWaaaaa@4CD1@ , por lo que se puede asegurar que la curva se sitúa por encima de la asíntotota.

Asíntotas oblicuas

Las funciones racionales,   f( x)= P( x) Q( x) MathType@MTEF@5@5@+=feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVC0de9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamOzamaabmaabaGaamiEaaGaayjkaiaawMcaaiabg2da9maalaaabaGaamiuamaabmaabaGaamiEaaGaayjkaiaawMcaaaqaaiaadgfadaqadaqaaiaadIhaaiaawIcacaGLPaaaaaaaaa@40AD@ , tienen asíntotas oblícuas cuando grado P − grado Q = 1, es decir, cuando el grado del numerador excede en una unidad al del denominador.

Para obtener la ecuación de la asíntota no hay más que efectuar la división de los polinomios.

En el ejemplo de la gráfica,   f( x)= x 3+2 x 2+x−4 2 x 2+2 MathType@MTEF@5@5@+=feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVC0de9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamOzamaabmaabaGaamiEaaGaayjkaiaawMcaaiabg2da9maalaaabaGaamiEamaaCaaaleqabaGaaG4maaaakiabgUcaRiaaikdacaWG4bWaaWbaaSqabeaacaaIYaaaaOGaey4kaSIaamiEaiabgkHiTiaaisdaaeaacaaIYaGaamiEamaaCaaaleqabaGaaGOmaaaakiabgUcaRiaaikdaaaaaaa@4749@   la división resulta: 

x 3+2 x 2+x−4 2 x 2+2 = 1 2x+1+ −6 2 x 2+2 = 12 x+1︸ asíntota oblícua − 3 x 2+1 MathType@MTEF@5@5@+=feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVC0de9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaSaaaeaacaWG4bWaaWbaaSqabeaacaaIZaaaaOGaey4kaSIaaGOmaiaadIhadaahaaWcbeqaaiaaikdaaaGccqGHRaWkcaWG4bGaeyOeI0IaaGinaaqaaiaaikdacaWG4bWaaWbaaSqabeaacaaIYaaaaOGaey4kaSIaaGOmaaaacqGH9aqpdaWcaaqaaiaaigdaaeaacaaIYaaaaiaadIhacqGHRaWkcaaIXaGaey4kaSYaaSaaaeaacqGHsislcaaI2aaabaGaaGOmaiaadIhadaahaaWcbeqaaiaaikdaaaGccqGHRaWkcaaIYaaaaiabg2da9maayaaabaWaaSaaaeaacaaIXaaabaGaaGOmaaaacaWG4bGaey4kaSIaaGymaaWcbaGaaeyyaiaabohacaqGTdGaaeOBaiaabshacaqGVbGaaeiDaiaabggacaqGGaGaae4BaiaabkgacaqGSbGaaey7aiaabogacaqG1bGaaeyyaaGccaGL44pacqGHsisldaWcaaqaaiaaiodaaeaacaWG4bWaaWbaaSqabeaacaaIYaaaaOGaey4kaSIaaGymaaaaaaa@6AEA@

La asíntota oblícua es entonces   y= 1 2x+1 MathType@MTEF@5@5@+=feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVC0de9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyEaiabg2da9maalaaabaGaaGymaaqaaiaaikdaaaGaamiEaiabgUcaRiaaigdaaaa@3B94@ , y la explicación es sencilla, pues para   x≫0 MathType@MTEF@5@5@+=feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVC0de9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiEaiablUMi=iaaicdaaaa@3883@ ,   x 3+2 x 2+x−4 2 x 2+2 = 1 2 x+1− 3 x 2+1 ≈ 1 2 x+1 MathType@MTEF@5@5@+=feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVC0de9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaSaaaeaacaWG4bWaaWbaaSqabeaacaaIZaaaaOGaey4kaSIaaGOmaiaadIhadaahaaWcbeqaaiaaikdaaaGccqGHRaWkcaWG4bGaeyOeI0IaaGinaaqaaiaaikdacaWG4bWaaWbaaSqabeaacaaIYaaaaOGaey4kaSIaaGOmaaaacqGH9aqpdaWcaaqaaiaaigdaaeaacaaIYaaaaiaaykW7caWG4bGaey4kaSIaaGymaiabgkHiTmaalaaabaGaaG4maaqaaiaadIhadaahaaWcbeqaaiaaikdaaaGccqGHRaWkcaaIXaaaaiabgIKi7oaalaaabaGaaGymaaqaaiaaikdaaaGaaGPaVlaadIhacqGHRaWkcaaIXaaaaa@5628@

Además, la diferencia o error cometido al aproximar la función mediante la asíntota,   − 3 x 2+1 MathType@MTEF@5@5@+=feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVC0de9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeyOeI0YaaSaaaeaacaaIZaaabaGaamiEamaaCaaaleqabaGaaGOmaaaakiabgUcaRiaaigdaaaaaaa@3AB6@ , es cada vez más pequeño a medida que aumenta x, y tiende a 0 cuando x tiende a infinito.

Para estudiar la posición de la curva respecto de la asíntota oblícua, de ecuación  y = mx + n, hay que analizar el signo de  f(x) − (mx + n)  cuando x≫0 MathType@MTEF@5@5@+=feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVC0de9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiEaiablUMi=iaaicdaaaa@3883@ . Si este resulta positivo la curva se encuentra por encima de la asíntota y si es negativo lo hará por debajo.

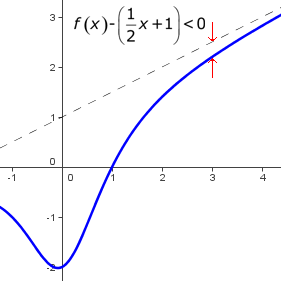
En el ejemplo de la gráfica,   f( x)−( mx+n )=−  3 x 2+1 <0 MathType@MTEF@5@5@+=feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVC0de9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamOzamaabmaabaGaamiEaaGaayjkaiaawMcaaiabgkHiTmaabmaabaGaamyBaiaadIhacqGHRaWkcaWGUbaacaGLOaGaayzkaaGaeyypa0JaeyOeI0IaaGPaVpaalaaabaGaaG4maaqaaiaadIhadaahaaWcbeqaaiaaikdaaaGccqGHRaWkcaaIXaaaaiabgYda8iaaicdaaaa@48B0@ , por lo que la curva se encuentra siempre por debajo de la asíntota (incluso cuando  x  tiende a menos infinito).