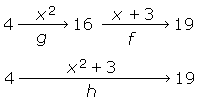Para la función h dada por h(x) = x2 + 3 , ¿cómo se calcula h(4) ?
No hay más que sustituir x por 4, h(4) = 42 + 3 , y realizar las operaciones indicadas:
- elevar 4 al cuadrado, 16
- al resultado anterior, 16, sumar 3, obteniendo 19.
Con una calculadora clásica:

Los pasos dados pueden esquematizarse:
4→ x2 16→ x+3 19 MathType@MTEF@5@5@+=feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqipu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaaGinamaaoqcaleaacaWG4bWaaWbaaWqabeaacaaIYaaaaaWcbeGccaGLsgcacaaIXaGaaGOnamaaoqcaleaacaWG4bGaey4kaSIaaG4maaqabOGaayPKHaGaaGymaiaaiMdaaaa@4142@
Si se consideran ahora las funciones
f(x) = x + 3 y g(x) = x2
resulta que la función h es la aplicación sucesiva de las funciones g y f (primero g y luego f), y se puede expresar
f(g(x)) = f(x2) = x2 + 3 = h(x)
COMPOSICIÓN DE FUNCIONES
Se llama función compuesta de f y g, y se expresa f∘g MathType@MTEF@5@5@+=feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqipu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamOzaiablIHiVjaadEgaaaa@38DE@ , a la función
x → f∘g f( g(x ) ) MathType@MTEF@5@5@+=feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqipu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiEaiaaysW7caaMe8UaaGjbVlaaysW7daGdKaWcbaGaaGjbVlaaysW7caaMe8UaaGjbVlaadAgacqWIyiYBcaWGNbGaaGjbVlaaysW7caaMe8UaaGjbVdqabOGaayPKHaGaaGjbVlaaysW7caaMe8UaaGjbVlaadAgadaqadaqaaiaadEgadaqadaqaaiaadIhaaiaawIcacaGLPaaaaiaawIcacaGLPaaaaaa@5A29@
Con lo que también se puede escribir
( f∘g ) ( x)=f( g( x) ) MathType@MTEF@5@5@+=feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqipu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaeWaaeaacaWGMbGaeSigI8Maam4zaaGaayjkaiaawMcaaiaaykW7daqadaqaaiaadIhaaiaawIcacaGLPaaacqGH9aqpcaWGMbWaaeWaaeaacaWGNbWaaeWaaeaacaWG4baacaGLOaGaayzkaaaacaGLOaGaayzkaaaaaa@4564@
|
En el ejemplo anterior
( f∘g ) (x )=f( g(x ) )=f( x2 )=x2 +3 MathType@MTEF@5@5@+=feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqipu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaeWaaeaacaWGMbGaeSigI8Maam4zaaGaayjkaiaawMcaaiaaykW7daqadaqaaiaadIhaaiaawIcacaGLPaaacqGH9aqpcaWGMbWaaeWaaeaacaWGNbWaaeWaaeaacaWG4baacaGLOaGaayzkaaaacaGLOaGaayzkaaGaeyypa0JaamOzamaabmaabaGaamiEamaaCaaaleqabaGaaGOmaaaaaOGaayjkaiaawMcaaiabg2da9iaadIhadaahaaWcbeqaaiaaikdaaaGccqGHRaWkcaaIZaaaaa@4F63@
o bien
( f∘g ) (x )=f( g(x ) )=g(x )+3=x2 +3 MathType@MTEF@5@5@+=feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqipu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaeWaaeaacaWGMbGaeSigI8Maam4zaaGaayjkaiaawMcaaiaaykW7daqadaqaaiaadIhaaiaawIcacaGLPaaacqGH9aqpcaWGMbWaaeWaaeaacaWGNbWaaeWaaeaacaWG4baacaGLOaGaayzkaaaacaGLOaGaayzkaaGaeyypa0Jaam4zamaabmaabaGaamiEaaGaayjkaiaawMcaaiabgUcaRiaaiodacqGH9aqpcaWG4bWaaWbaaSqabeaacaaIYaaaaOGaey4kaSIaaG4maaaa@5010@
ATENCIÓN: La composición de funciones NO es conmutativa. 
|