MODELO DE DISTRIBUCIÓN BINOMIAL
Observemos el siguiente enunciado:
|
El
departamento de Matemática Aplicada
propone un examen de test consistente en 25 cuestiones.
Cada cuestión tiene 5 respuestas listadas. Si un estudiante no
conoce la respuesta correcta de ninguna cuestión prueba
suerte, queremos saber: |
Piensa un poco como plantearlo.......
En primer lugar hay que identificar el problema con la
distribución binomial

Si
queremos responder a la primera pregunta P(X=7):
Secuencia
de comandos:
En
la ventana encontramos tres opciones:
Probability: Dado un valor de la variable aleatoria, da la probabilidad de que la variable tome dicho valor, en el caso de variables discretas o, para variables continuas, proporciona la ordenada de la función de densidad.
Cumulative probability: dado un valor de la variable aleatoria, da la probabilidad acumulada o función de distribución:
Inverse cumulative probability: Dada
una probabilidad, calcula el valor de la variable aleatoria que
presenta esa probabilidad acumulada o valor de la función de distribución
Ventana:
En Probability
En
la pantalla de sesión nos sale el resultado
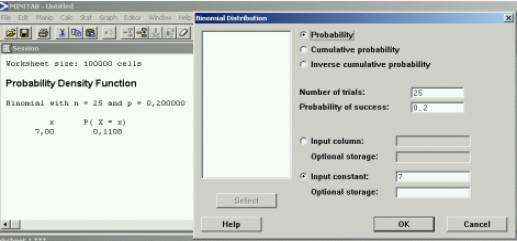
Si
ahora queremos responder a la segunda
pregunta b) como la probabilidad de
acertar como mínimo 9 cuestiones es hallar la probabilidad P(X<=9):
Secuencia:
Calc/Probability Distributions/binomial.
Cumulative
probability
Introducimos
los datos trials n=25 y Probability p=1/5.
P(X<=9): input constant escribe 9
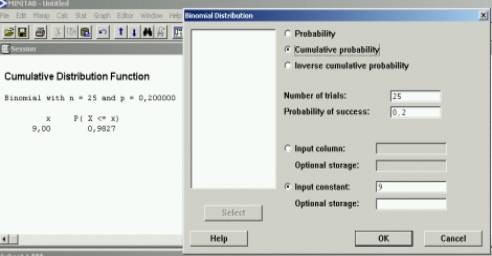
Para la tercera cuestión la probabilidad de aprobar sería
probabilidad de acertar al menos 13 cuestiones: P(X>=13), como
Minitab solo nos halla la probabilidad acumulada (PX<=13), tendremos
que aplicar la propiedad de la probabilidad complementaria: P(X>=13)
= 1-P(X<13) =1-P(X<=12), luego hallamos P(X<=12) y lo
restamos de 1.
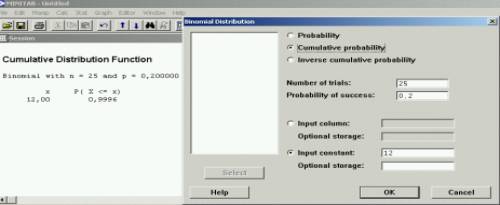
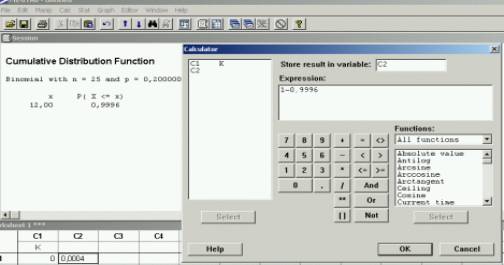
luego el resultado es : 0,0004.
Ejemplo: Se sabe que después del incendio que asoló Santander en 1941, el 45% de los hogares están asegurados contra
incendios. Una compañia de Seguros quiere realizar una encuesta para
estudiar el mercado, para lo cual selecciona 7 hogares de la ciudad.
Hallar:
1º Probabilidad de que tres hogares estén
asegurados.
2º Probabilidad de que a lo sumo sean 4 los
asegurados.
3º Probabilidad de que al menos 2 estén asegurados.
4º Probabilidad de que no haya ninguno asegurado.
5º Probabilidad de que alguno esté asegurado.
Solución :
Identificar el problema:
Cuando
escogemos un hogar puede suceder :
Que esté asegurado, suceso A tal que p(A)=0,45.
Que no esté asegurado, suceso A' tal que p(A')=0,55
Además que un hogar esté asegurado, es independiente de que lo estén los demás.
Luego
X=nº de hogares asegurados al escoger 7 hogares es una variable
aleatoria que sigue una distribución binomial, con n=7 y p=0,45
B(7, 0,45).
Contestamos
a las preguntas:
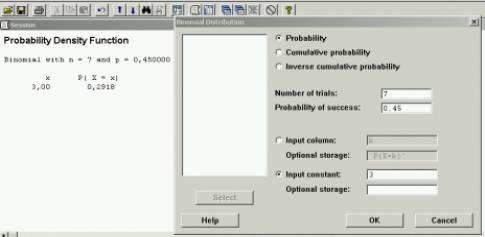
1º)
Es hallar la P(X=3)=0,2918
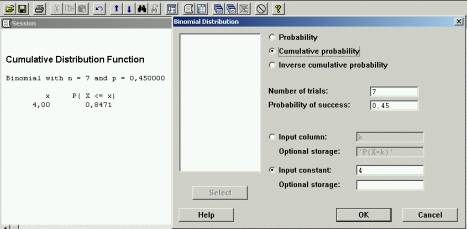
2º) Buscamos
P(X<=4)=0,8471
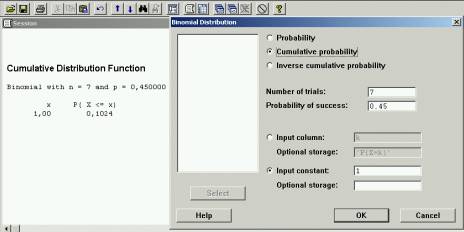
3º)
P(X>=2)=1-P(X<2)=1-P(X<=1)=1-0,1024=0,8976
4º) P(X=0)=0,0152
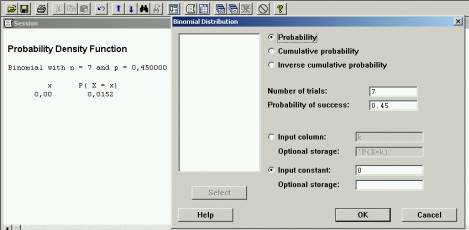
5º) P(X>0)=1-P(X<=0)=1-P(X=0)=1-0,0152=0,9848