Si
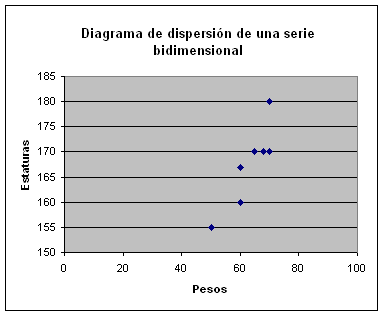
observamos la nube de puntos del ejemplo de la página anterior
notaremos que los puntos se agrupan alrededor de una línea recta
indicando que existe entre ambas variables una cierta dependencia
"lineal". A la recta que "mejor" se "ajusta" a la nube se le llama recta de regresión, la estudiaremos más adelante.
Se denomina coeficiente
de correlación a un coeficiente (que definimos más adelante) que mide
lo bien que se ajustan los puntos a la recta en cuestión.
|
La correlación puede ser
-
positiva,
si la pendiente de la recta es positiva. Un ejemplo
es el caso del ejemplo superior, a más peso más
estatura.
-
negativa, si la pendiente de la recta es negativa.
Por ejemplo a más partidos perdidos menos puntos.
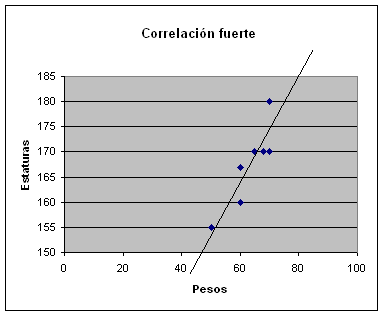
Finalmente, como se aprencia
en el gráfico superior los puntos se sitúan bastante próximos a la recta que se
representa en este caso se dirá que la correlación entre la
variable peso y la altura es alta o fuerte.
|
|
Ejemplo: Si
consideramos la nota que han sacado nuestros alumnos en Matemáticas
y representamos la variable bidimensional Peso - Nota de Matemáticas,
cuyos valores son:
(60, 5), (65, 5), (65, 9), (65,4),
(70, 8), (70,3), (70,6), (70,5), (70,7), (70,6), (65, 4), (65,2), (68, 5),
(68,4), (50, 6), (60,6)
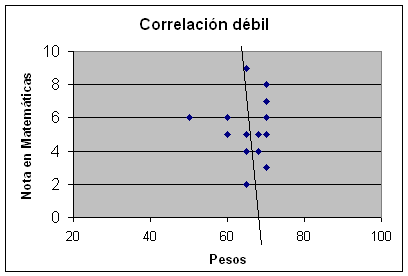
se obtiene el gráfico de la derecha.
En este gráfico no se observa tendencia a que los datos se agrupen alrededor de
ninguna recta, o si acaso, alrededor de una recta de pendiente cero. Por lo
tanto, la correlación es muy débil, lo cual refleja el hecho de que hay muy poca
dependencia entre la nota de Matemáticas y el peso del alumno. Se dice que son dos
variables incorreladas.
|
 |
|
|