Así, si
f:D⊆
ℝ
2
→ℝ
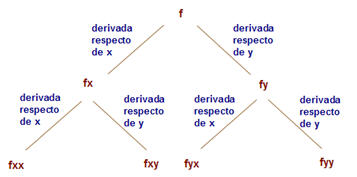
es una función de dos variables que tiene derivadas parciales respecto de x y de y en todos los puntos de D, quedan definidas dos nuevas funciones
f
x
,
f
y
:D⊆
ℝ
2
→ℝ
.
Si las derivadas parciales de estas funciones existen se
pueden definir las derivadas parciales de orden 2.
|
∂
∂x
(
∂z
∂x
)=
∂
2
z
∂
x
2
=
z
xx
''
(
x,y
)=
f
xx
''
(
x,y
)=
lim
Δx→0
z
x
'
(
x+Δx,y
)−
z
x
'
(
x,y
)
Δx
∂
∂y
(
∂z
∂x
)=
∂
2
z
∂x∂y
=
z
xy
''
(
x,y
)=
f
xy
''
(
x,y
)=
lim
Δy→0
z
x
'
(
x,y+Δy
)−
z
x
'
(
x,y
)
Δy
∂
∂y
(
∂z
∂y
)=
∂
2
z
∂
y
2
=
z
yy
''
(
x,y
)=
f
yy
''
(
x,y
)=
lim
Δy→0
z
y
'
(
x,y+Δy
)−
z
y
'
(
x,y
)
Δy
∂
∂x
(
∂z
∂y
)=
∂
2
z
∂y∂x
=
z
yx
''
(
x,y
)=
f
yx
''
(
x,y
)=
lim
Δx→0
z
y
'
(
x+Δx,y
)−
z
y
'
(
x,y
)
Δx
De la misma manera podrían definirse las derivadas de orden 3, 4, etc.
|
