La derivabilidad de una función supone un progreso en relación con la simple continuidad de una función; se trata de una condición más restrictiva, ya que existen funciones continuas que no son derivables.

Es decir

Si f(x) es derivable en x = a entonces f(x) es continua en x = a

El teorema recíproco no es cierto

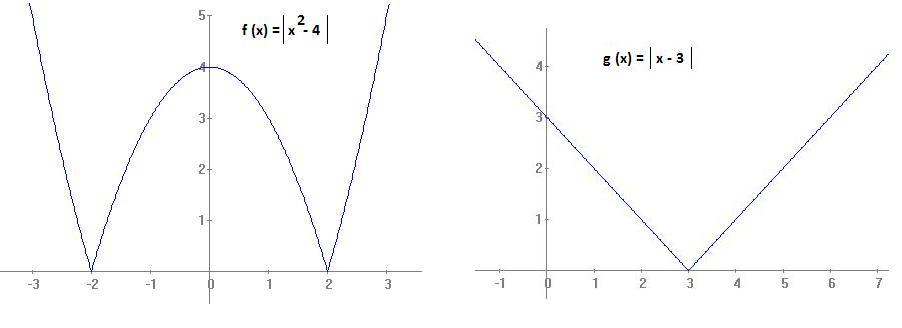
Por regla general, cualquier función no será derivable en lo que llamamos punto anguloso.
Un punto anguloso es un punto de la gráfica en el que se produce un cambio brusco de pendiente.
Por ejemplo: f (x) = |  x 2  - 4  |  y g(x) = |  x -3  |

f(x) es continua en todo R y no es derivable en x =-2 y x = 2 ; g(x) es continua en todo R y no es derivable en x = 3