Interferencias ondas

Composición de dos M.A.S. de la misma dirección y frecuencia. Interferencia de ondas.

La composición de movimientos armónicos simples ( M.A.S.) se basa en la relación existente entre el M.A.S y el movimiento circular uniforme y es importante para explicar la interferencia de dos movimientos ondulatorios armónicos. Compondremos dos M.A.S. de la misma dirección y frecuencia, el primero con amplitud A1, y fase inicial ϕ 1 x 1 = A 1 ⋅cos    (ωt+ ϕ 1 ) el segundo con amplitud A2, y fase inicial ϕ 2 x 2 = A 2 ⋅cos    (ωt+ ϕ 2 ) El resultado es un M.A.S. de la misma dirección y de la misma frecuencia x = A ⋅cos    (ωt+ ϕ ) La amplitud y fase inicial se pueden obtener a partir de la figura, sumando los vectores rotatorios que representan a cada uno de los dos M.A.S. componentes. A → = A → 1 + A → 2 Se consideran dos situaciones importantes: 1) Dos M.A.S. están en fase si la diferencia de fase es cero ( ϕ 1 − ϕ 2 = 0 º ) , el M.A.S resultante tiene una amplitud que es la suma de las amplitudes de los dos M.A.S. 2) Dos M.A.S. están en oposición de fase si la diferencia de fase es ϕ 1 − ϕ 2 =±    180 º , el M.A.S resultante tiene una amplitud que es la diferencia de las amplitudes de los dos M.A.S.   Actividades

Experimento de interferencia de Young de la rendija doble

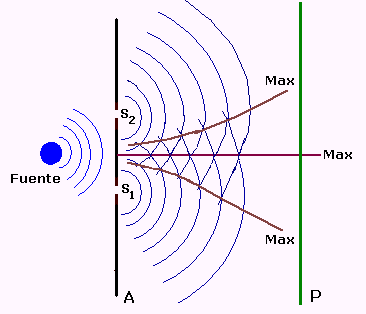
Una de las características esenciales del movimiento ondulatorio es el fenómeno de la interferencia. Consideremos una fuente luminosa monocromática (emite una sola longitud de onda), tal como muestra la figura4 La luz procedente de la fuente monocromática incide sobre la pantalla A, la cual tiene dos rendijas angostas, paralelas e idénticas, S1 y S2 que están separadas una distancia a. Supongamos que la fuente equidista de las dos rendijas. En estas condiciones, las ondas que salen por las rendijas tienen la misma frecuencia angular ω , y están en fase. 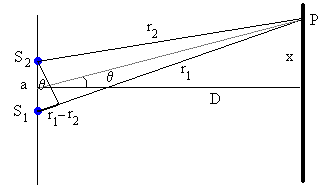La intensidad de la luz que se observa sobre la pantalla P consta de una serie de bandas paralelas, alternativamente brillantes y oscuras, denominadas franjas interferenciales de Young, como muestra la imagen   Sobre la figura 5 podemos observar que una onda procedente de la ranura inferior recorre una distancia mayor que la onda que sale de la rendija superior, en una cantidad a⋅sen    θ . Esta distancia es la diferencia de trayectoria δ , donde δ= r 1 − r 2 =a⋅sen    θ   Las ondas que salen de S1 y S2 describen un M.A.S. cuyas ecuaciones son, respectivamente: ψ 1 = A 1 ⋅sen   (  k   r 1 −ωt) ψ 2 = A 2 ⋅sen   (  k   r 2 −ωt) Los casos más importantes que pueden darse son:   En fase o interferencia constructiva. 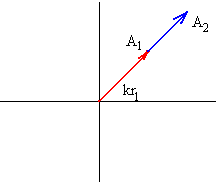Dos M.A.S están en fase cuando la diferencia de fase kr1-kr2 es un múltiplo entero de 2  π . Teniendo en cuenta que k= 2  π λ k   r 1 −k   r 2 =2  n  π          ⇒           r 1 −   r 2 =n  λ La amplitud resultante es la suma de amplitudes A=A1+A2 En oposición de fase o interferencia destructiva. 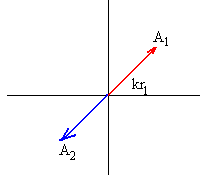Dos M.A.S están en oposición de fase cuando la diferencia de fase kr1-kr2 es un múltiplo impar de π . Teniendo en cuenta que k= 2  π λ k    r 1 −k    r 2 =(2n+1)   π          ⇒           r 1 −    r 2 = (2n+1) 2    λ La amplitud resultante es la diferencia de amplitudes. Si ambas son iguales, el punto P no se mueve. Resumiendo, las condiciones de interferencia son Interferencia constructiva    r 1 −   r 2 =n   λ Interferencia destructiva r 1 −   r 2 = 2n+1 2    λ Amplitud resultante La amplitud resultante de la interferencia de las dos ondas anteriores se obtiene fácilmente utilizando notación compleja, en decir representando las ondas como vectores en el plano complejo. Tendremos en cuenta que ψ 1 =Im   [ A 1 ⋅ e i  (k   r 1 −ωt) ] ψ 2 =Im   [ A 2 ⋅ e i  (k   r 2 −ωt) ] Definimos los vectores: A → 1 = A 1 ⋅ e i  (k   r 1 −ωt) A → 2 = A 2 ⋅ e i  (k   r 2 −ωt) Es necesario sumar los vectores A → 1    y     A → 2   para obtener la amplitud resultante: A → =  A 1 ⟶   + A 2 ⟶ A= ( A 1 ) 2 + ( A 2 ) 2 +2   A 1    A 2 ⋅cos   (k   r 1 −k   r 2 ) Como en el experimento de Young las amplitudes A1 y A2 son iguales, podemos escribir A=  2   ( A 1 ) 2 ⋅[   1+cos  (k   r 1 −k   r 2 )   ]        A=  4   ( A 1 ) 2 ⋅cos    2 ( k   r 1 −k   r 2 2 )                  A= 2     A 1 ⋅cos     ( k   r 1 −k   r 2 2 ) donde r 1 − r 2 =a  ⋅sen  θ A partir de esta expresión podemos hallar las direcciones θ   para las cuales la interferencia es constructiva o destructiva Interferencia constructiva a⋅sen   θ=n   λ Interferencia destructiva a⋅sen   θ= 2n+1 2    λ También podemos hallar las posiciones x sobre la pantalla, que registran interferencia constructiva y destructiva, para ello hacemos la aproximación siguiente: si el ángulo θ  es pequeño, sen   θ≈tg   θ= x D Interferencia constructiva a  x D =n  λ Interferencia destructiva a  x D = 2n+1 2   λ Intensidad La intensidad de un movimiento ondulatorio es proporcional al cuadrado de la amplitud, de modo que I=4    I 0 ⋅ cos 2 α          ⇒          α= π   a λ    sen   θ I es la intensidad resultante en el punto P  e I0 es la intensidad en dicho punto P debida a la onda luminosa procedente de una sola de las rendijas. En la interferencia constructiva α=n   π  y por tanto la intensidad I=4I0. En cambio, en la interferencia destructiva α=(2n+1)  ⋅ π 2  y la intensidad I=0.   Interferencia  constructiva  I=22 I0. Interferencia destructiva  I=0. Es importante señalar que en la interferencia constructiva la intensidad en P debida a las dos fuentes es 22 veces la que corresponde a una de las fuentes.   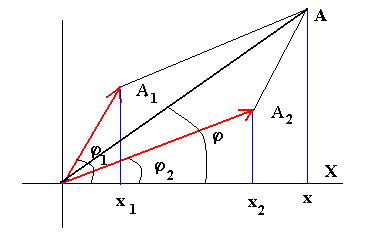Diagrama de fasores:  Consideremos dos ondas luminosas senoidales cuyas componentes del campo eléctrico sean A1 y A2. La figura 6 representa el diagrama de fasores para varios valores de la diferencia de fase φ , y los valores correspondientes a la diferencia de trayectoria δ , que se obtienen a partir de la ecuación φ= 2π λ ⋅δ= 2π λ ⋅a⋅sen    θ   La intensidad será máxima cuando la amplitud resultante A sea máxima. Esto ocurre cuando los valores del ángulo son  ϕ=0, 2π, 4π ,  etc. Análogamente, se observa que la intensidad será cero cuando A sea cero. El primer punto de intensidad cero sucede en φ= 180 º , lo que corresponde a δ= λ 2 , mientras que los otros puntos de intensidad nula suceden para φ=  π,     3π,     5π,     etc. Estos resultados se demostraron anteriormente de forma analítica. La ventaja del método de los fasores frente al método analítico es mayor cuando se necesitan sumar varias ondas, procedentes de n rendijas. En la figura 7 se muestra cómo se halla el fasor resultante de la interferencia de cuatro ondas luminosas A → =  A → 1 + A → 2 + A → 3 + A → 4 El fasor A es el resultante de los cuatro fasores de igual amplitud. La fase de A es   α con respecto al primer fasor.

Cerrar la ventana y volver al Módulo Principal