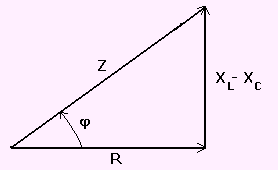Circuitos

Elementos de un circuito de corriente alterna. Cálculo de la potencia.

Un circuito de corriente alterna consta de una combinación de elementos (resistencias, capacidades y autoinducciones) y un generador que suministra la corriente alterna. Una fuerza electromotriz (f.e.m.) alterna se produce mediante la rotación de una bobina con velocidad angular constante ω dentro de un campo magnético uniforme producido entre los polos de un imán. La f.e.m. o diferencia de potencial alterna producida en la bobina se expresa así v= V 0    sen   (ωt) donde V0 es la amplitud del voltaje o diferencia de potencial máxima, v es la diferencia de potencial instantánea y ω es la velocidad angular o pulsación, igual a  2π veces la frecuencia F. Para analizar los circuitos de corriente alterna se emplea un procedimiento geométrico denominado de vectores rotatorios o fasores, que se basa en la notación vectorial de los números complejos. De este modo, se representa la función senoidal anterior por una expresión compleja de la forma V= V 0 ⋅cos  (ωt)+j⋅ V 0 ⋅sen  (ωt)= V 0 ⋅ e   j ω t donde, para cada instante t,  V es un número complejo de módulo el valor eficaz V0 y argumento α=ω  t . Según este procedimiento, V es un vector cuya longitud representa la amplitud o valor máximo V0 y su proyección sobre el eje vertical representa el valor instantáneo de dicha magnitud, v. Los vectores se hacen girar en sentido contrario al de las agujas del reloj con velocidad angular ω, siendo el ángulo de fase ω t, en un instante dado. Los valores de la amplitud se representan con letras mayúsculas y los valores instantáneos con letras minúsculas.

Una resistencia conectada a un generador de corriente alterna

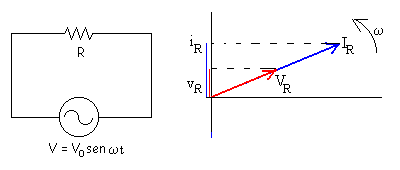
La ecuación de este circuito simple es (intensidad por resistencia igual a la f.e.m.) i⋅R= V 0    sen   (ωt) i R = V 0 R ⋅   sen   (ωt) La diferencia de potencial en la resistencia es v R = V 0 ⋅   sen   (ωt) En una resistencia, la intensidad iR y la diferencia de potencial vR están en fase. La relación entre sus amplitudes es I R = V R R Como vemos en la representación vectorial de la figura, al cabo de un cierto tiempo t, los vectores rotatorios que representan a la intensidad y a la diferencia de potencial entre los extremos de la resistencia, han girado un ángulo ω t.  Sus proyecciones sobre el eje vertical, marcados por los segmentos de color azul y rojo, son respectivamente los valores en el instante t de la intensidad que circula por la resistencia y de la diferencia de potencial entre sus extremos.

Un condensador conectado a un generador de corriente alterna

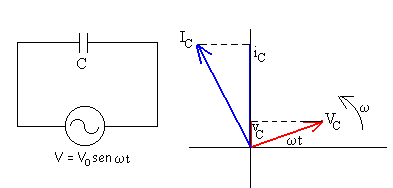
En un condensador la carga q, la capacidad C y diferencial de potencial v entre sus placas están relacionadas entre sí q=C⋅v Si se conectan las placas del condensador a un generador de corriente alterna q=C⋅ V 0   sen   (ωt) La intensidad se obtiene derivando la carga respecto del tiempo, i = dq/dt i C =C⋅ω⋅ V 0    cos   (ωt)=C⋅ω⋅ V 0    sen   ( ωt+ π 2 ) Para un condensador, la intensidad iC está adelantada 90º respecto a la diferencia de potencial vC, tal como muestra el diagrama vectorial de la figura. La relación ente sus amplitudes es I C =C⋅ω⋅ V C Los máximos de intensidad tienen lugar un cuarto de periodo antes que los correspondientes máximos de voltaje. La intensidad máxima puede escribirse  I C = V C 1/ωC = V C X C donde  X C = 1 ωC   es la reactancia capacitiva del condensador (se mide en ohmios, Ω ).

Una bobina conectada a un generador de corriente alterna

Cuando circula una corriente i variable con el tiempo por una bobina, se produce una corriente autoinducida, debido al fenómeno de autoinducción. Suponemos que la autoinducción de la bobina es L, entonces la diferencia de potencial entre los extremos de la bobina es igual a L⋅ d  i d  t . La ecuación del circuito se obtiene igualando a cero la suma de las fuerzas electromotrices, ya que la resistencia es nula.  −L⋅ d  i d  t + V 0 ⋅sen   (ω  t)=0          ⇒           d  i d  t = V 0 L ⋅sen   (ω  t) Integrando esta ecuación obtenemos i en función del tiempo i    L =− V 0 ω  L ⋅cos   (ωt)= V 0 ω  L ⋅sen   ( ωt− π 2 ) La intensidad iL en la bobina está retrasada 90º respecto de la diferencia de potencial entre sus extremos vL, tal como muestra la figura. La relación entre sus amplitudes es I   L = V L ω  L = V L   X L donde X L =ω  L   es la reactancia inductiva de la bobina (se mide en ohmios, Ω ). Actividades

Circuito serie R-L-C

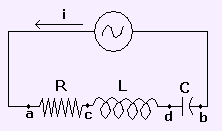
La figura 1 muestra un circuito serie sencillo, que posee una resistencia, una reactancia inductiva y una reactancia capacitiva.   La intensidad instantánea i tiene el mismo valor en todos los puntos del circuito. 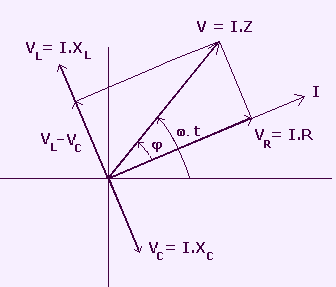El voltaje total a través de los tres elementos es igual al voltaje del generador, y el vector V que los representa es la suma vectorial de los vectores que corresponden a los voltajes individuales:   VR = I.R ,  VL = I.XL ,  VC = I.XC  El diagrama vectorial completo se muestra en la figura 2    En el diagrama se tienen en cuenta las siguientes propiedades:  El voltaje en la resistencia, VR, está en fase con el vector intensidad I. El voltaje VL está adelantado 90º respecto a la intensidad I.  El voltaje VC se halla retrasado 90º con relación a I.  Para formar la suma vectorial, restamos primero el vector VC del vector VL y obtenemos VL- VC , que es perpendicular a VR. La amplitud del voltaje V resultante verifica:  V=   V R  2 + ( V L − V C ) 2 =I⋅   R 2 + ( X L − X C ) 2 La suma algebraica de los tres voltajes máximos  VR + VL + VC es una cantidad sin sentido físico, que resulta mucho mayor que el voltaje máximo V del generador. Esto se debe a que cuando sumamos funciones sinusoidales como los voltajes instantáneos  vR , vL , vC , deben tenerse en consideración tanto sus amplitudes como sus fases.  Dado que los tres potenciales tienen distinta fase, aunque la suma de los tres nos proporcionaría el voltaje máximo V = vR + vL + vC  este cálculo sería más costoso que usando el método de los fasores anterior.  Definimos la impedancia Z del circuito, basándonos en la expresión anterior de V, como Z=    R 2 + ( X L − X C ) 2    ,          luego          V=I⋅Z La impedancia nos da la razón entre la amplitud del voltaje y la amplitud de la intensidad, así como el ángulo de fase entre las ondas de voltaje y corriente. La impedancia se mide en ohmios, Ω . La diferencia de fase entre el voltaje V y la intensidad I en la línea, se deduce de la figura 3,  que se denomina triángulo de impedancia del circuito RLC, así tg    φ= V L − V C V R = X L − X C R La expresión general de la potencia media suministrada a un circuito de corriente alterna se define como un producto de versores: P med = 1 2 ⋅V⋅I⋅cos   φ El factor  cos   φ   se denomina factor de potencia del circuito. La potencia media puede expresarse P med = V ef ⋅ I ef ⋅cos   φ donde Vef e Ief  son los valores eficaces (valores rms) del voltaje y de la intensidad, respectivamente. Estos valores eficaces son los que realmente miden los instrumentos de medida en corriente alterna; se definen como el valor máximo de esa magnitud divididio por  2 .   Problema

Cerrar la ventana y volver al Módulo Principal