La integral definida como límite
Cuando el límite de las sumas (para n tendiendo a infinito) existe, se dice que la función es integrable. Este límite es la integral definida de f(x) entre a y b, y se indica ∫ a b f(x)dx MathType@MTEF@5@5@+=feaafiart1ev1aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaa8qmaeaacaWGMbGaaiikaiaadIhacaGGPaGaamizaiaadIhaaSqaaiaadggaaeaacaWGIbaaniabgUIiYdaaaa@3F0B@ .
Las funciones continuas son integrables, pero no son las únicas con esta propiedad.
Por lo tanto, si f(x)≥0 MathType@MTEF@5@5@+=feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamOzaiaacIcacaWG4bGaaiykaiabgwMiZkaaicdaaaa@3BAE@  para a≤x≤b MathType@MTEF@5@5@+=feaafiart1ev1aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyyaiabgsMiJkaadIhacqGHKjYOcaWGIbaaaa@3C22@ , entonces ∫ a b f(x)dx MathType@MTEF@5@5@+=feaafiart1ev1aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaa8qmaeaacaWGMbGaaiikaiaadIhacaGGPaGaamizaiaadIhaaSqaaiaadggaaeaacaWGIbaaniabgUIiYdaaaa@3F0B@  nos da el área debajo de la gráfica.
Aquí hemos introducido la integral definida como límite de las sumas inferiores, pero luego veremos un método directo para calcular la integral definida usando una primitiva.
Hay otras clases de sumas que se pueden usar para definir la integral, como se explica en el nivel 3.

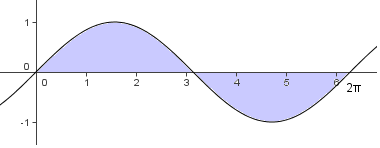
Funciones con valores negativos
Si la función f(x) toma valores positivos y valores negativos, en la integral, las áreas que están por encima del eje-x cuentan como positivas y las áreas que están por debajo del eje-x cuentan como negativas. Como consecuencia, puede ocurrir que la integral valga cero aunque la función no sea constantemente cero.
Por ejemplo, ∫ 0 2π sin⁡x dx =0 MathType@MTEF@5@5@+=feaafiart1ev1aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaa8qmaeaaciGGZbGaaiyAaiaac6gacaWG4baccaGae8hiaaIaamizaiaadIhaaSqaaiaaicdaaeaacaaIYaGaeqiWdahaniabgUIiYdGccqGH9aqpcaaIWaaaaa@439E@ , pues el área entre 0 y π y el área entre π y 2π son iguales en valor absoluto, pero mientras que la primera es positiva, la segunda es negativa.

Propiedades de la integral definida
Supondremos que f(x) MathType@MTEF@5@5@+=feaafiart1ev1aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamOzaiaacIcacaWG4bGaaiykaaaa@392F@  y g(x) MathType@MTEF@5@5@+=feaafiart1ev1aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaam4zaiaacIcacaWG4bGaaiykaaaa@3930@  son continuas en el intervalo de la integral.