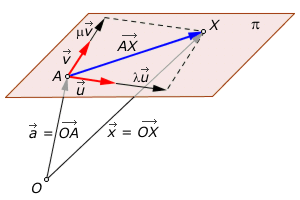
Un plano, p, queda determinado cuando se conocen un punto, A, y dos vectores   u→   y  v→ MathType@MTEF@5@5@+=feaaguart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLw BLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc 9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGabmyDayaalaG aaeiiaiaabccacaqG5bGaaeiiaiaabccaceWG2bGbaSaaaaa@3B93@   paralelos al mismo (vectores de dirección o vectores directores).

¿Qué condición habrá de cumplir un punto X del espacio para que pertenezca al plano p?

El punto X estará sobre el plano cuando, y solo cuando, el vector   AX → MathType@MTEF@5@5@+=feaaguart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzY bItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0Firpepe KkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaa8HaaeaacaWGbbGaamiwaaGaay51Gaaaaa@3949@   sea combinación lineal de   u→   y  v→ MathType@MTEF@5@5@+=feaaguart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLw BLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc 9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGabmyDayaalaG aaeiiaiaabccacaqG5bGaaeiiaiaabccaceWG2bGbaSaaaaa@3B93@ . Así pues, habrán de existir números reales l y m tales que:

AX → =λ u→ +μv → MathType@MTEF@5@5@+=feaaguart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhi ov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0 xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaa8HaaeaacaWGbbGaamiwaaGaay 51GaGaeyypa0Jaeq4UdWMabmyDayaalaGaey4kaSIaeqiVd0MabmODayaalaaaaa@40B4@

Fijado un sistema de referencia con origen en O se tiene:

OX→ = OA→ + AX → x→ =a → + AX → MathType@MTEF@5@5@+=feaaguart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9w DYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepa e9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGceaqabeaadaWhcaqaaiaad+eacaWGybaacaGLxdcacqGH9 aqpdaWhcaqaaiaad+eacaWGbbaacaGLxdcacqGHRaWkdaWhcaqaaiaadgeacaWGybaacaGLxdcaaeaaceWG4bGbaSaacqGH9aqpceWGHbGb aSaacqGHRaWkdaWhcaqaaiaadgeacaWGybaacaGLxdcaaaaa@4931@

y, en definitiva:

Establecido el sistema de referencia es posible sustituir los vectores de la ecuación por sus coordenadas:

( x, y,  z )=( a 1 , a2 , a3 ) +λ( u1 , u2 ,  u3 ) +μ( v1 , v2 ,  v3 ) ( x,  y, z )=( a1 +λu1 + μv1 ,  a2 +λu 2 +μv2 , a3 + λu3 +μ v3 ) MathType@MTEF@5@5@+=feaaguart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBL nhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqa qpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGceaqabeaadaqadaqaaiaad IhacaGGSaGaaGjbVlaadMhacaGGSaGaaGjbVlaadQhaaiaawIcacaGLPaaacqGH9aqpdaqadaqaaiaadggadaWgaaWcbaGaaGymaaqabaGccaGGS aGaaGjbVlaadggadaWgaaWcbaGaaGOmaaqabaGccaGGSaGaaGjbVlaadggadaWgaaWcbaGaaG4maaqabaaakiaawIcacaGLPaaacqGHRaWkcqaH7 oaBdaqadaqaaiaadwhadaWgaaWcbaGaaGymaaqabaGccaGGSaGaaGjbVlaadwhadaWgaaWcbaGaaGOmaaqabaGccaGGSaGaaGjbVlaadwhadaWga aWcbaGaaG4maaqabaaakiaawIcacaGLPaaacqGHRaWkcqaH8oqBdaqadaqaaiaadAhadaWgaaWcbaGaaGymaaqabaGccaGGSaGaaGjbVlaadAhad aWgaaWcbaGaaGOmaaqabaGccaGGSaGaaGjbVlaadAhadaWgaaWcbaGaaG4maaqabaaakiaawIcacaGLPaaaaeaadaqadaqaaiaadIhacaGGSaGaa GjbVlaadMhacaGGSaGaaGjbVlaadQhaaiaawIcacaGLPaaacqGH9aqpdaqadaqaaiaadggadaWgaaWcbaGaaGymaaqabaGccqGHRaWkcqaH7oaBc aWG1bWaaSbaaSqaaiaaigdaaeqaaOGaey4kaSIaeqiVd0MaamODamaaBaaaleaacaaIXaaabeaakiaacYcacaaMe8UaamyyamaaBaaaleaacaaIY aaabeaakiabgUcaRiabeU7aSjaadwhadaWgaaWcbaGaaGOmaaqabaGccqGHRaWkcqaH8oqBcaWG2bWaaSbaaSqaaiaaikdaaeqaaOGaaiilaiaay sW7caWGHbWaaSbaaSqaaiaaiodaaeqaaOGaey4kaSIaeq4UdWMaamyDamaaBaaaleaacaaIZaaabeaakiabgUcaRiabeY7aTjaadAhadaWgaaWcb aGaaG4maaqabaaakiaawIcacaGLPaaaaaaa@98E9@

Resultando:

ECUACIONES PARAMÉTRICAS DEL PLANO r: { x= a 1+λ u 1+μ v 1 y= a 2+λ u 2+μ v 2 z= a 3+λ u 3+μ v 3 MathType@MTEF@5@5@+=feaaguart1ev2aaatCvAUfeBSjuyZL2y d9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0 Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr =xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamOCaiaacQdadaGabaqaauaabaqadeaaaeaacaWG4bGae yypa0JaamyyamaaBaaaleaacaaIXaaabeaakiabgUcaRiabeU7aSjaadwhadaWgaaWcbaGaaGymaaqabaGccqGHRaWk cqaH8oqBcaWG2bWaaSbaaSqaaiaaigdaaeqaaaGcbaGaamyEaiabg2da9iaadggadaWgaaWcbaGaaGOmaaqabaGccqG HRaWkcqaH7oaBcaWG1bWaaSbaaSqaaiaaikdaaeqaaOGaey4kaSIaeqiVd0MaamODamaaBaaaleaacaaIYaaabeaaaO qaaiaadQhacqGH9aqpcaWGHbWaaSbaaSqaaiaaiodaaeqaaOGaey4kaSIaeq4UdWMaamyDamaaBaaaleaacaaIZaaab eaakiabgUcaRiabeY7aTjaadAhadaWgaaWcbaGaaG4maaqabaaaaaGccaGL7baaaaa@5F78@

Si en el sistema anterior se toman l y m como incógnitas:

{ u 1 λ+ v 1μ =x− a 1 u 2λ+ v 2 μ=y− a 2 u 3λ+ v 3μ=z− a 3 MathType@MTEF@5@5@+=feaaguart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2Caerbu LwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9L q=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaiqaa eaafaqaaeWabaaabaGaamyDamaaBaaaleaacaaIXaaabeaakiabeU7aSjabgUcaRiaadAhadaWgaaWcbaGaaGymaaqabaGccqaH8oqBcqGH9 aqpcaWG4bGaeyOeI0IaamyyamaaBaaaleaacaaIXaaabeaaaOqaaiaadwhadaWgaaWcbaGaaGOmaaqabaGccqaH7oaBcqGHRaWkcaWG2bWaa SbaaSqaaiaaikdaaeqaaOGaeqiVd0Maeyypa0JaamyEaiabgkHiTiaadggadaWgaaWcbaGaaGOmaaqabaaakeaacaWG1bWaaSbaaSqaaiaai odaaeqaaOGaeq4UdWMaey4kaSIaamODamaaBaaaleaacaaIZaaabeaakiabeY7aTjabg2da9iaadQhacqGHsislcaWGHbWaaSbaaSqaaiaai odaaeqaaaaaaOGaay5Eaaaaaa@5DE4@

Para que el sistema, de tres ecuaciones con dos incógnitas, tenga solución, el rango de la matriz ampliada ha de ser dos, y su determinante cero:

| u1 v 1 x− a1 u2 v 2 y− a2 u3 v 3 z− a3 |=0MathType@MTEF@5 @5@+=feaaguart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDha rqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0Firpep eKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaqWaaeaafaqabeWadaaabaGaamyDamaaBaaaleaacaaIXaaabe aaaOqaaiaadAhadaWgaaWcbaGaaGymaaqabaaakeaacaWG4bGaeyOeI0IaamyyamaaBaaaleaacaaIXaaabeaaaOqaaiaadwhadaWgaaW cbaGaaGOmaaqabaaakeaacaWG2bWaaSbaaSqaaiaaikdaaeqaaaGcbaGaamyEaiabgkHiTiaadggadaWgaaWcbaGaaGOmaaqabaaakeaa caWG1bWaaSbaaSqaaiaaiodaaeqaaaGcbaGaamODamaaBaaaleaacaaIZaaabeaaaOqaaiaadQhacqGHsislcaWGHbWaaSbaaSqaaiaai odaaeqaaaaaaOGaay5bSlaawIa7aiabg2da9iaaicdaaaa@51BF@     

Al desarrollar el determinante resulta:

ECUACIÓN GENERAL O IMPLÍCITA DEL PLANO Ax+By +Cz+D= 0MathType@MTEF@5@5@+=feaaguart1ev2aaatCv AUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rN CHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0Firp epeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyqaiaadIhacqGHRaWkcaWGcbGaamyEaia bgUcaRiaadoeacaWG6bGaey4kaSIaamiraiabg2da9iaaicdaaaa@4070@

Hay, por último, otra forma de la ecuación del plano denominada segmentaria que resulta muy interesante de cara a la representación gráfica del plano.

Sorry, the GeoGebra Applet could not be started. Please make sure that Java 1.4.2 (or later) is installed and active in your browser (Click here to install Java now)

Pincha y arrasta sobre el punto X y se irán mostrando los distintos valores de los parámetros λ y μ.

Creado con GeoGebra