En apartados anteriores ("base y coordenadas") se establecía, dada una base
B={
u→ 1,
u→ 2,
u→ 3
}
MathType@MTEF@5@5@+=feaaguart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtub
sr4rNCHbGeaGqiVC0de9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGa
ciGaaiaabeqaamaabaabaaGcbaGaamOqaiabg2da9maacmaabaGabmyDayaalaWaaSbaaSqaaiaaigdaaeqaaOGaaiilaiaaysW7ceWG1bGbaSaadaWgaaWcbaGaaG
OmaaqabaGccaGGSaGaaGjbVlqadwhagaWcamaaBaaaleaacaaIZaaabeaaaOGaay5Eaiaaw2haaaaa@43E6@
, la "asociación" entre vectores y coordenadas:
a→
=x u →
1 +y
u →2 +z
u →3 ︸
vector
↔
( x, y,
z )︸
coordenadas
MathType@MTEF@5@5@+=feaaguart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVC0de9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGa
aiaabeqaamaabaabaaGcbaWaaGbaaeaaceWG1bGbaSaacqGH9aqpcaWG4bGaaGPaVlqadwhagaWcamaaBaaaleaacaaIXaaabeaakiabgUcaRiaadMhacaaMc8UabmyD
ayaalaWaaSbaaSqaaiaaikdaaeqaaOGaey4kaSIaamOEaiqadwhagaWcamaaBaaaleaacaaIZaaabeaaaeaacaqG2bGaaeyzaiaabogacaqG0bGaae4BaiaabkhaaOGa
ayjo+dGaaGjbVlaaysW7daGd4aWcbeqaaaGccaGLugcacaaMe8UaaGjbVpaayaaabaWaaeWaaeaacaWG4bGaaiilaiaaykW7caWG5bGaaiilaiaaykW7caWG6baacaGL
OaGaayzkaaaaleaacaqGJbGaae4Baiaab+gacaqGYbGaaeizaiaabwgacaqGUbGaaeyyaiaabsgacaqGHbGaae4CaaGccaGL44paaaa@69E3@
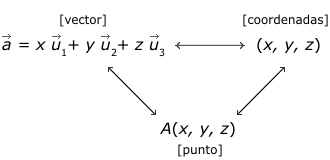
Es preciso completar esa asociación añadiendo los "puntos", a fin de poder emplear, indistintamente, puntos, vectores
o coordenadas:
|
¿Cómo asociar puntos con vectores y coordenadas?
Imagínate una región del espacio (conjunto de puntos del espacio) que observamos a través de la ventana que se muestra
a la derecha.
|

|
|
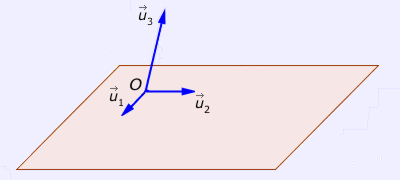
Tomamos un punto cualquiera de esa región y lo etiquetamos con la letra O; a este punto se le llamará ORIGEN.
Una vez fijado el origen, O, tomamos representantes de los vectores
u →1
,
u →2
y
u →3
de la base que tengan origen en O.
El artilugio ya está preparado para asociar los puntos con vectores y coordenadas.
(El plano que aparece en la figura, sobre el que se encuentran los vectores
u →1
y
u →2
, se muestra únicamente para dar una idea de perspectiva, profundidad o vista
tridimensional)
|
|
|
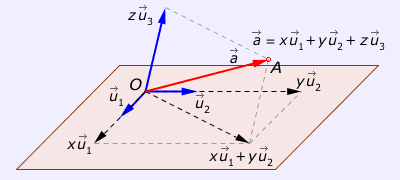
Es el momento de tomar un punto A cualquiera.
A este punto se le asocia el vector
OA→
, VECTOR DE POSICIÓN del punto A, y las coordenadas (x, y, z)
del vector referidas a la base.
(x, y, z) serán así tanto coordenadas del vector
OA
→
como coordenadas del punto A.
El vector de posición de un punto suele escribirse con la misma letra, en minúsculas, que el punto:
a→
=OA→
|
|
Se ha establecido, así, una asociación que permite "describir" un punto a través de sus coordenadas referidas a un
origen y a una base. Mientras no cambiemos el origen y la base, la descripción es única.
- A cada punto le corresponde un vector (vector de posición) y unas coordenadas.
- A cada vector le corresponden unas coordenadas y un punto (su extremo o afijo).
- A cada terna (x, y, z) le corresponde un vector y un punto.
Además, puesto que la descripción es única, conocida una de las representaciones
(punto, vector o coordenadas) se pueden obtener las otras dos.
|
SISTEMA DE REFERENCIA
Es el conjunto formado por un punto O, origen, y una base
B={
u→ 1,
u→ 2,
u→ 3
}
MathType@MTEF@5@5@+=feaaguart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtub
sr4rNCHbGeaGqiVC0de9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGa
ciGaaiaabeqaamaabaabaaGcbaGaamOqaiabg2da9maacmaabaGabmyDayaalaWaaSbaaSqaaiaaigdaaeqaaOGaaiilaiaaysW7ceWG1bGbaSaadaWgaaWcbaGaaG
OmaaqabaGccaGGSaGaaGjbVlqadwhagaWcamaaBaaaleaacaaIZaaabeaaaOGaay5Eaiaaw2haaaaa@43E6@
del plano vectorial:
R={ O
, { u
→ 1,
u→ 2,
u→ 3
} }
MathType@MTEF@5@5@+=feaaguart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDh
arqqtubsr4rNCHbGeaGqiVC0de9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr
=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamOuaiabg2da9maacmaabaGaam4taiaacYcacaaMe8+aaiWaaeaaceWG1bGbaSaadaWgaaWcbaGaa
GymaaqabaGccaGGSaGaaGjbVlqadwhagaWcamaaBaaaleaacaaIYaaabeaakiaacYcacaaMe8UabmyDayaalaWaaSbaaSqaaiaaiodaaeqaaaGccaGL7bGa
ayzFaaaacaGL7bGaayzFaaaaaa@4938@
|
Una vez establecido un sistema de referencia podemos referirnos a un punto a través de su vector de posición o a través
de sus coordenadas.
Si la base es ortonormal, también el sistema de referencia se llama ortonormal. Siempre que se escriban unas
coordenadas se entenderá que están referidas, mientras no se indique otra cosa, a un sistema ortonormal.
El establecimiento de un sistema de referencia permitirá, en las páginas siguienes, obtener
las primeras aplicaciones prácticas.
|



