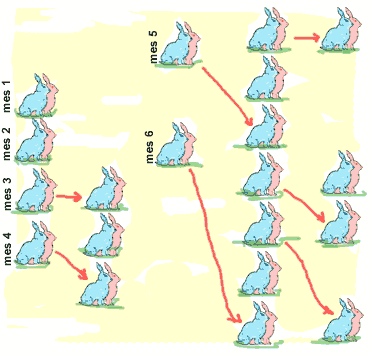
Hace muchos años, en 1202, Fibonacci se planteó el siguiente problema: Supongamos que tenemos una pareja de conejos macho y hembra de un mes de edad que aún no pueden reproducirse, pero que podrán hacerlo cuando cumplan dos meses de edad. Supongamos también que cada mes, a partir del segundo, nace una nueva pareja de conejos (macho y hembra. Si cada pareja de conejos se reproduce de la misma forma que la pareja inicial, ¿cuántas parejas habrá al principio de cada mes?
Este planteamiento no es muy real, por ejemplo en el caso de que en el proceso de reproducción se dé la tendencia de tener más conejos que conejas o viceversa, ya no se lograría el equilibrio de parejas conejo-coneja, o si los conejos se mueren, ... Sin embargo existen ejemplos más reales.
El matemático Henry E. Duedeney (1857-1930) propuso uno de estos ejemplos utilizando vacas y toros.
Otro ejemplo tiene que ver con las abejas. Según se sabe, una vez inseminada la abeja reina por un zángano (de otro enjambre), aquella se queda en su colmena y ya no sale más, dedicándose a la puesta de huevos que ella misma va fecundando o no, dando origen así a abejas obreras o reinas, en el primer caso, y machos o zánganos en el segundo caso. Si observamos el árbol genealógico de un zángano, podemos ver cómo el número de abejas en cada generación es uno de los términos de la sucesión de Fibonacci. En efecto, los machos no tienen padre, por lo que él sólo tendrá dos abuelos —los padres de la reina—, tres bisabuelos —porque el padre de la reina no tuvo padre—, cinco tatarabuelos y ocho tataratatarabuelos.