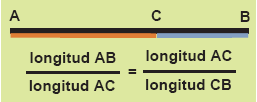La razón áurea

Razón áurea

Muchas veces habrás oído decir que cierto objeto está o no está proporcionado. Nos referimos a las relaciones que mantienen las distintas partes. Por ejemplo una mano puede ser grande pero estar proporcionada con el cuerpo de la persona.

Los griegos pensaron sobre la forma más armónica de dividir un segmento cualquiera en dos partes desiguales y estimaron que la mejor de ellas era aquella en la que al comparar el segmento completo con la mayor de las partes resultara el mismo valor que al comparar la mayor de las partes con el más pequeño.

Este valor es la razón áurea y vale 1+ 5 2 ≃1'618

Rostro en proporción áurea:

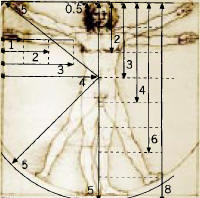
Cuerpo en proporción áurea: En "el hombre ideal", Leonardo da Vinci estableció lo que consideró las proporciones humanas más perfectas. En el dibujo de la izquierda, la relación entre algunas de las medidas principales del cuerpo humano es la áurea. Por ejemplo, el cociente entre el lado del cuadrado y el radio de la circunferencia que tiene por centro el ombligo, es el número de oro

Veamos algunos ejemplos donde está presente la razón aúrea:

Arte:

Apolo de Belvedere. Los lados del rectángulo en el cual está idealmente inscrita la estatua del Apolo de Belvedere están relacionados según la sección áurea, es decir, con una proporción de 1:1,618.

El cuadro de Dalí "Leda atómica", pintado en 1949, sintetiza siglos de tradición matemática y simbólica, especialmente pitagórica. Se trata de una filigrana basada en la proporción áurea, pero elaborada de tal forma que no es evidente para el espectador. En el boceto de 1947 se advierte la meticulosidad del análisis geométrico realizado por Dalí basado en el pentagrama místico pitagórico

Cuadro de Dalí: "Media taza gigante suspendida con incomprensible apéndice de cinco metros"

Construcción: El número áureo ha sido utilizado desde la época de los egipcios para la construcción de edificios, si bien, son los griegos los que lo explotaron al máximo usando en todas las facetas del arte. A continuación se detallan algunos ejemplos de este uso.

Pirámide de Keops: El primer uso conocido del número áureo en la construcción aparece en la pirámide de Keops, que data del 2600 a.C..	Esta pirámide tiene cada una de sus caras formadas por dos medios triángulos áureos: la más aparente, aunque no la única, relación armónica identificable en el análisis de las proporciones de este monumento funerario en apariencia simple.
El Partenón	Un ejemplo de rectángulo áureo en el arte es el alzado del Partenón griego. En la figura se puede comprobar que AB/CD=. Hay más cocientes entre sus medidas que dan el número áureo, por ejemplo: AC/AD= y CD/CA=.
El Templo de Ceres	El Templo de Ceres en Paestum (460 a.C.) tiene su fachada construida siguiendo un sistema de triángulos áureos, al igual que los mayores templos griegos, relacionados, sobre todo, con el orden dórico.
La Tumba Rupestre de Mira en Asia Menor basa su construcción en un pentágono áureo, en el que el cociente de la diagonal y el lado de dicho pentágono es el número áureo.

El DNI o documento nacional de identidad.

Stradivarius utilizaba el número de oro en la construcción de sus famosos violines.

Bolsa: Los números de Fibonacci se ajustan bastante bien a periodos y ciclos bursátiles. Cuando un valor de bolsa ha empezado a cambiar su tendencia después de algunos días subiendo o bajando de forma clara, se puede prever que la corrección será del 61.8 % (observa los decimales de 1/φ y compáralos con los de φ , donde φ es la razón áurea. ¿Qué observas?) o del 38.2% ( 1−φ ). Son las llamadas líneas de Fibonacci, tenidas muy en cuenta por los analistas de mercados financieros. También se aplican para tratar de identificar cambios en las tendencias de mercado y se dibujan en periodos de tiempo proporcionales a 5, 8, 13, 21, ...